递归算法(一)
10 June 2020
To iterate is human,to recurse divine.—— L. Peter Deutsch
递归(英语:Recursion),又译为递回,在数学与计算机科学中,是指在函数的定义中使用函数自身的方法. 通俗的说就是”自我相似性”, 递归涉及将一个结构嵌套在另一个结构中,或者将一个序列嵌入另一个结构中,无论是文字、事件还是物理对象的序列。
递归贯穿于各种文化,贯穿于科学、数学和艺术之中。它就像树上的树枝或空中的泡泡一样的常见. 同时它又对人类的思考和沟通方式也至关重要.
递归具体表现为以下两个属性:
- 循环嵌套: 一遍又一遍的重复,而每次重复都嵌套在上一次的重复之中.
- 自身构建: 在循环嵌套的过程中,每次重复的是由同一个“自身”(代表着结构和模式)所构成的。
自然界中的递归
线性递归:
下一层的递归只有一个, 并且嵌套与上一层的递归,最常见的就是螺旋线, 线条基于其起点的位置一次又一次的递归扩大或缩小,最终形成一条完美的螺旋线.
这种曲线出现在:鹦鹉螺贝壳,玫瑰花瓣,蛛网… 中

螺旋线外形的贝壳

西兰花: 它的外形是一个天然的近似分形。
分叉递归:
在自然界中更加多见的,无处不在的是分叉递归. 在上一层的递归基础上, 下一层分叉出去. 其中比较容易理解的就是树枝的分, 空气泡泡的分叉,还有雪天的迹等等…

在几个球型的泡泡之间会有多个小气泡,在几个小气泡之间又有几个小小气泡…
 雪迹的递归: 雪迹的边缘线会在原来的基础上分叉出去, 然后新产生的边缘线又在原来的基础上继续分叉…
雪迹的递归: 雪迹的边缘线会在原来的基础上分叉出去, 然后新产生的边缘线又在原来的基础上继续分叉…
 一棵树,它的树干是我们容易看到的,如果我们再细看树干上分叉出来的树枝,会发现它的结构、比例与树干很像,树枝上再分叉出更细小的枝桠,这枝桠的结构、比例也与树枝、树干很像,如此类推下去,就是一棵树上的递归现象。
一棵树,它的树干是我们容易看到的,如果我们再细看树干上分叉出来的树枝,会发现它的结构、比例与树干很像,树枝上再分叉出更细小的枝桠,这枝桠的结构、比例也与树枝、树干很像,如此类推下去,就是一棵树上的递归现象。
 大尺度的山脉、河床,也很清晰的可以看到分叉递归
大尺度的山脉、河床,也很清晰的可以看到分叉递归
 甚至整个银河系.
甚至整个银河系.
…
其他学科领域的递归
语言学的递归
语言的递归性指“语言结构层次和言语生成中相同结构成分的重复或相套”. 递归性是语言学中非常重要的概念, 它影响着人类的思维模式.
语言的句子是无穷无尽的,而语法规则却是有限的, 人们之所以能够借助于有限的语法规则,造出无穷无尽的句子来,其原因就在于语言符号具有递归性。
拿汉语来说, 汉语的句法构造的递归性突出地表现为句法成分所特有的套叠现象。在汉语里,由实词和实词性词语组合而成的任何一种类型的句法结构,其组成成分本身,又可以由该类型的句法成分充任,而无须任何的形态标志。这种套叠现象在主谓结构、偏正结构、述宾结构、述补结构、联合结构、复谓结构中都是存在的。这是由语言符号的递归性导致的汉语语法的一个重要特点。
例如,在句子“他嗓子疼”,中,“嗓子/疼”是主谓结构,这个主谓结构套叠在“他嗓子疼”中做谓语,与“他”又构成一个更大的主谓结构“他/嗓子疼”,这是主谓结构的套叠现象。
又如,在短语“北大数学老师”中,“数学/老师”是偏正结构,这个偏正结构套叠在 “北大数学教师”中,与它前面的名词“北大”又构成一个更大的偏正结构“北大/数学老师”,这是偏正结构的套叠现象。这些套叠现象都反映出汉语语法的递归性特点。
在自然语言处理的研究中,语言符号的递归性起着很大的作用。机器翻译的实质,就是把源语言中无限数目的句子,通过有限的规则,自动地转换为目标语言中无限数目的句子。 如果机器翻译的规则系统不充分利用语言符号的递归性,要实现这样的转换是非常困难的,甚至是不可能的。
生物学的递归
在生物学上有进化树的概念, 而树的概念在文章前面已经提到过是一种递归现象. 递归过程是我们从简单的生物体到具有无限可能的思想的复杂生物的关键。 它是描述几乎任何类型的进步或进化的方式之一。
数学中的递归
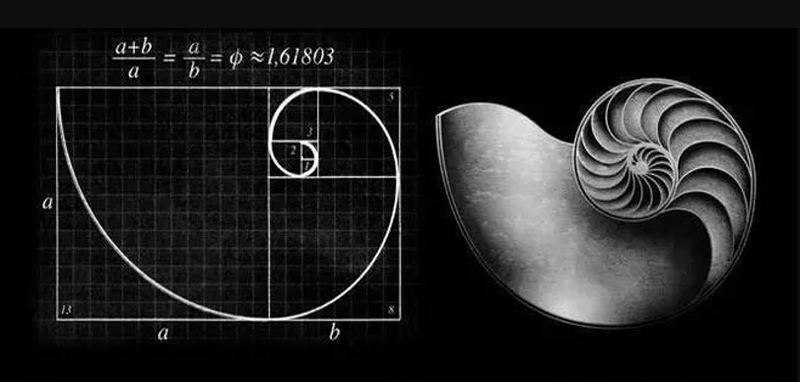
斐波那契螺旋线,也称“黄金螺旋”,作图规则是在以斐波那契数( Fibonacci Sequence )为边的正方形拼成的长方形中画一个90度的扇形,连起来的弧线就是斐波那契螺旋线。
谢尔宾斯基三角形: 由波兰数学家谢尔宾斯基在1915年提出。它是自相似集的例子。
- 取一个实心的三角形。(多数使用等边三角形)
- 沿三边中点的连线,将它分成四个小三角形。
- 去掉中间的那一个小三角形。
- 对其余三个小三角形重复1。
一个谢尔宾斯基三角形也可由一棵分形树勾勒出来的,三个分支之间形成60°角的分形树。如果角度减小,三角形可以不断地转化为类似于树的分形。

科赫曲线:给定线段AB,科赫曲线可以由以下步骤生成:
- 将线段分成三等份(AC,CD,DB)
- 以CD为底,向外(内外随意)画一个等边三角形DMC
- 将线段CD移去
- 分别对AC,CM,MD,DB重复1~3。
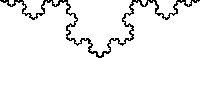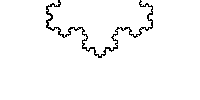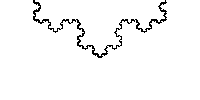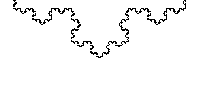
递归的实质
从一般意义上说,递归方法是一种从简单到复杂、从低级到高级的可连续可操作的方法。
它的每一步骤 都是可行可操作的,各步骤之间又是连续的。
通过这种方法, 可以用简单的、自明的要素描述、构造、说明复杂的整体。
从而通过解决简单的问题来解决复杂的问题。
Reference
- L Peter Deutsch: The founder of Aladdin Enterprises and creator of Ghostscript, a free software PostScript and Portable Document Format interpreter. Deutsch’s other work includes the Smalltalk implementation that inspired Java just-in-time compilation technology about 15 years later.
- https://www.longdom.org/open-access/recursive-evolution-a-tale-of-natural-id-2332-0915-1000189.pdf
- https://medium.com/@daniel.oliver.king/getting-started-with-recursion-f89f57c5b60e
- https://recursivecurve.wordpress.com/2016/11/23/hilbert-curve-and-recursion/
- http://www.lingviko.net/feng/8-features-final.pdf
相关文章
建筑师编程课推广
ikuku精选课 Python4Rhino 建筑师编程课 2020.5.16开始线上直播!讲师:马海东

Python4Rhino递归案例1
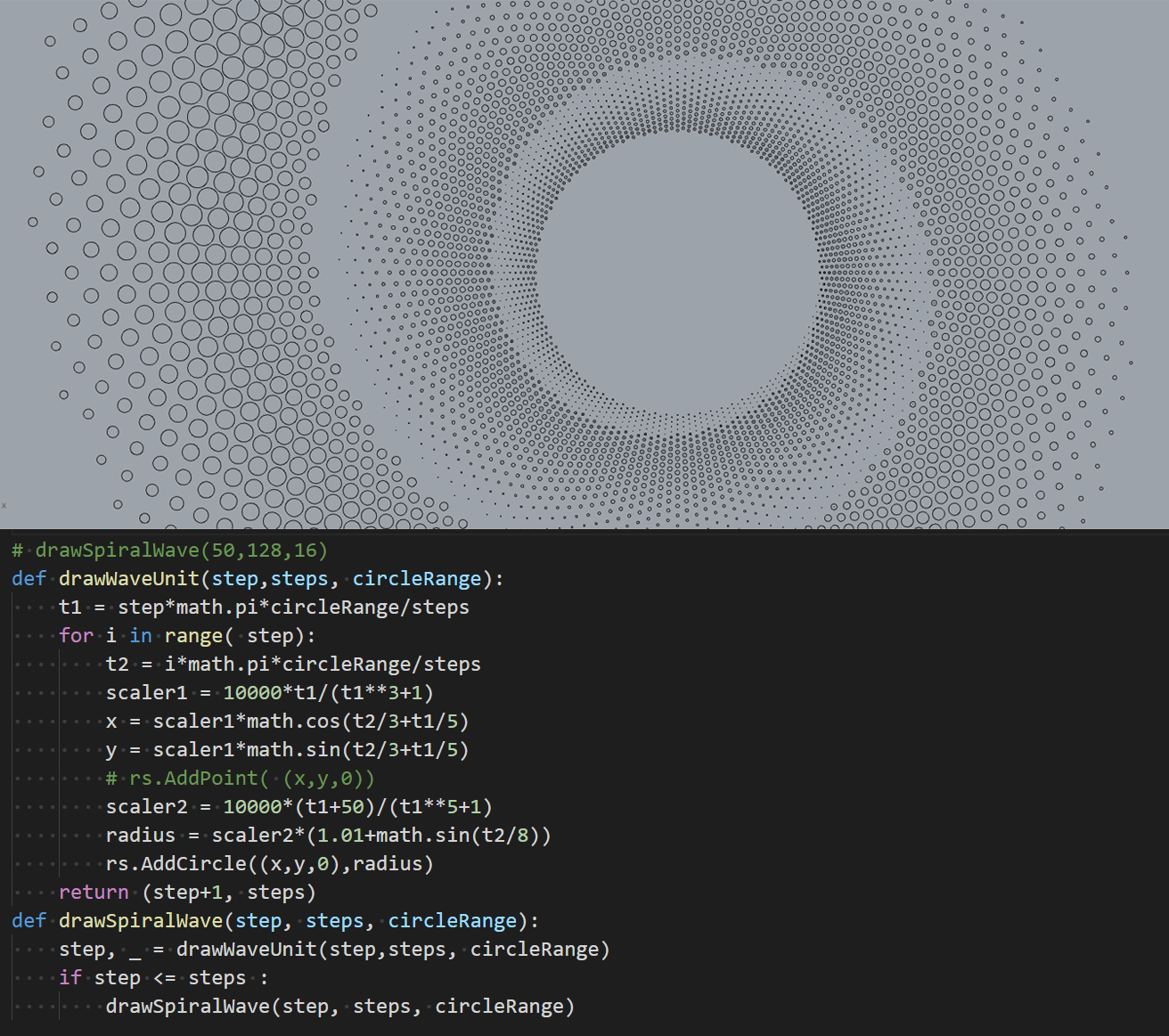
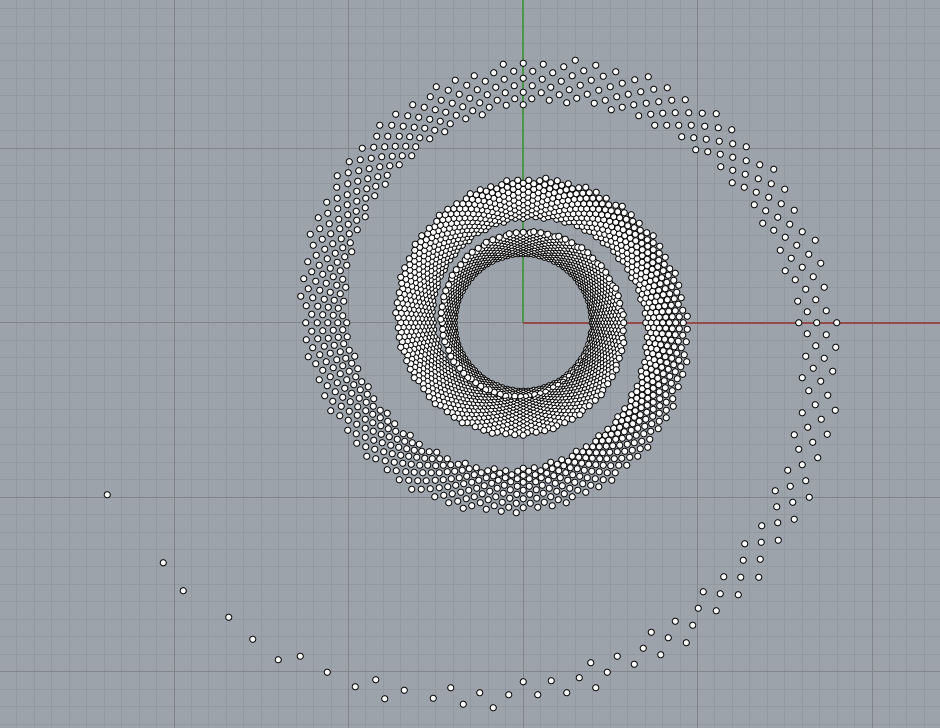

Python4Rhino递归案例2

Comments
No comments found for this article.
Join the discussion for this article on this ticket. Comments appear on this page instantly.