作者: Alastair Townsend (经过作者亲自授权)
英文网址: http://www.alatown.com/spline-history-architecture

中文整理: 马海东 ,并提供了一个deboor曲线算法的grasshopper插件(见文末的下载链接)

一些建筑师将采用自由曲面设计和计算机辅助制造技术称为前沿，甚至是前卫。虽然在建筑设计领域内可能是这样，但事实上，这些技术本质上并没有什么新意。与其他领域的同行相比，建筑师事实上已经落后于其他领域。本文试图通过总结计算曲线的巧妙发展，来解决这种知识上的不足，而这一切都发生在其他行业中。
这是一个引人入胜的故事。
任何一个只需点击几下鼠标就能画出曲线的设计师，可能都会从了解这项技术–我们现在认为是理所当然的技术–是如何发展起来而受益匪浅。

半个多世纪前，在计算机数控制造(CNC)领域,计算出三维曲面的需求是第一个计算机辅助设计（CAD）软件诞生的动力，其动力主要来自汽车和航空工业。 而娱乐行业的数字动画师们开发出了直观地平滑拓扑模糊形式的方法。这些解决方案已经迁移到今天建筑师们使用的软件工具中。 然而，曲率的历史显然早在计算时代之前就已经有了。它可以追溯到我们早期祖先最原始的努力，将自然材料按照人类的意愿进行弯曲。

曲率一直在建筑中发挥着重要的结构作用，在罗马的拱门和圆顶建筑中就很明显，这些拱门和圆顶建筑至今仍然屹立不倒。 弯曲的形式贯穿于建筑史，一直延续到现代，其中Antonin Gaudí的悬链拱顶、Félix Candela的薄壳屋顶和Frei Otto的拉伸双曲面抛物线就是显著的例子。 曲率也对建筑产生了美学上的影响。例如，在希腊古代，内敛性的使用使柱子在荷载的作用下显得凸起。现代主义50年代和60年代，曲线建筑在经历了相对短暂的全盛时期后，到了20世纪末，曲线建筑已经退潮，只有少数非主流的设想者在其中领航。Frank Gehry的标志性的毕尔巴鄂古根海姆博物馆（1997年）改变了这一切。它预示着一场曲线形的形式主义文艺复兴，并向主流文化宣告了当代数字建筑时代的到来。值得一提的是，NURBS（Non-Uniform Rational B-Splines）软件–特别是Dessault的Catia®–用来构思和协调博物馆起伏的钛合金表皮的建造，是最初为设计战斗机而开发的技术。 Catia和NURBS的起源都可以追溯到20世纪60年代的巴黎，在那里，计算曲线几乎同时在两家竞争对手的汽车工厂中发明了。而 “spline”一词–今天几乎成为计算机曲线的同义词–可以追溯到早期的海上制船业，它最初是指一种灵活的木条，用于划定船体的平滑横截面–这种技术(lofting)从古代就开始使用。我们今天使用的计算机建模词汇中仍然保留着这些术语，这并不是巧合。

鉴于目前建筑中的自由曲面的流行，以及人体工程学形式在我们日常生活中的广泛流行–从牙刷到自行车头盔–似乎很少有关于21世纪计算机辅助设计的几何学基础的历史研究（建筑或其他方面），这一点让人惊讶。 从平凡到崇高，spline划分了当代美学（曲线和直线），因为它是设计、工程和制造行业的通用语言。然而，它的历史仍然没有得到足够的重视，它的技术基础通常没有被理解，即使是那些热衷于采用spline的人，他们也不太了解，因为他们倾向于认为现代3D软件的点击式操作是理所当然的。

大多数关于早期的计算机辅助几何设计（CAGD）的描述都来自于（主要是学术性的）书籍和论文，这些书籍和论文都是为该领域内的高技术观众而写的。除了一、两个明显的例外[i]，历史上的发展都是作为数学方程的演进来介绍的，没有对其对人类更广泛的重要性作过多的评论。 这些文本假定要有高深的数学知识，可悲的是，作者并不具备这一点。因此，这本书可能是第一本为用户群体–即设计师–的直观理解和利益而写的非技术性的花键故事。 具体来说，对于建筑师来说，值得我们熟悉spline对更广泛的设计领域的影响，以便将当代建筑发展置于一个更有历史和技术基础的背景下。 我希望，解开曲线的神秘面纱，将有助于对现在已经成为事实上的建筑工具:spline——形成更好的鉴赏力，甚至是鉴赏家。

从弓到船 - 机械spline

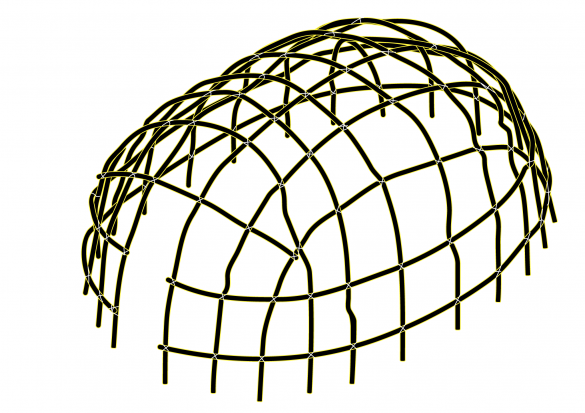
图1：来自中石器时代定居点的证据，以及像美洲土著人本土棚屋结构所示，这是一种最简单的住所形式，是将杆子夯成圆形，向内弯曲，然后将它们捆绑在一起，形成一个坚固的圆顶花格。

到了中石器时代，人类已经学会了用弓来狩猎。当猎人拉弓时，弓的两端被拉近，产生更大的弯曲度。当木材变形时，木材会储存弹性势能，因为木材试图恢复原来的直线度。木材的天然弹性使树木能够长高，但又不会在风中弯曲而折断。当一长段木材弯曲时，凹面的材料会受到压缩，而凸面的材料则受到拉力。在弯曲过程中，这些力尽可能均匀地分布在整个木材的长度上，从而产生一个最佳的平滑曲线。

中石器时代定居点的证据以及许多土著文化的证据显示，原始的住所是以类似的方式建造的[ii]。相对立的两根树杆的顶部被钉在一起，形成一个整体的穹顶状的花格子，并被兽皮、树皮或草覆盖。每根木杆的弹性产生了一个拱形，这是一个最佳的结构形状，在受压的情况下，给原始的穹顶赋予了强度和刚性（见图1）。

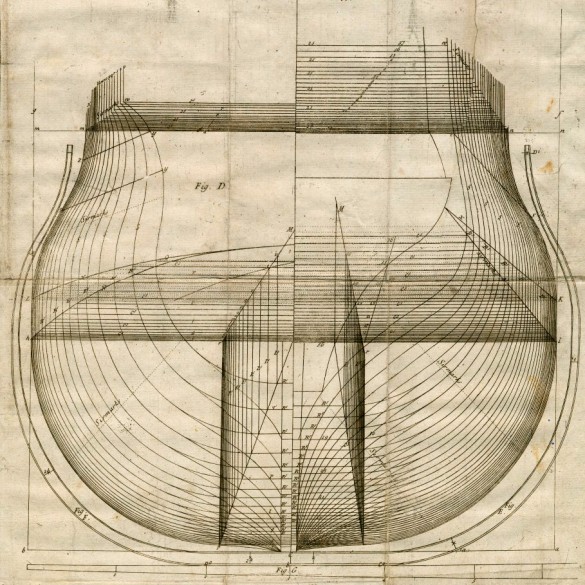
图2：由叠加建造几何形状组成的船体平面图。像这样的横断面记录了合同订单上的船舶。外侧构件（标有图E/F）是中舱模具。每个横断面的部分都与可重构模具上的相应部件有索引。 资料来源。来源：William Sutherland, The Shipbuilders Assistant: or, Some Essays Towardsting the Art of Marine Architecture (London, 1711), 82。

自古以来，人类就利用弧形物体的固有实用性，不仅满足了人类的基本吃住需求，还能满足人类的交通需求。从粗略的意义上说，船就是前面提到的原始小屋的简单倒置。当外皮或其他外层用柏油做了防水层后，人们就有了一个基本的（尽管不稳定）小船。后来，经过几千年的演变，船的设计和构造也在水、风、船速的动力学作用下得到了精简。

罗马人使用全尺寸的木制模板，或者说是模具，制造出可变的木制肋骨来加固他们的船体[iii]。当铺上木板时，这些骨架肋骨支撑着船体的光滑轮廓(见图2)。每根肋骨的弯曲轮廓都是由可重构的主模板绘制出来的，该模板由一块块弧形和直木片组成。模板上的刻度线标明了每根肋骨的位置。利用这种早期的参数化方法，可以用一个模板制造出一个相同的船队。

图3：被称为 “ducks”的钩状砝码，可以准确地固定一条spline–在这里，仅仅一条薄薄的桦木条–用于描画船体。资料来源：Edson International

这种做法在整个地中海北部地区一直延续到17世纪[iv]。随着造船从一门手艺发展到一门科学，图纸取代了全尺寸的木制模板。绘制肋骨和龙骨图案的做法被称为lofting设计，因为车间上方的阁楼(loft)是唯一的干燥无遮挡的地面空间，足以容纳1:1的定型过程。长长的曲线是由一条薄薄的柔性木条或钢筋划到木材上，称为spline（见图3）。spline是由一系列三个或更多的钩状金属砝码（称为鸭子）弯曲并固定在一个平面上。当长的弹性spline努力恢复其原始的直线度时，整个弹性spline的应力分布均匀，保证了最佳的平滑、美观和机械上的良好曲率。这种均匀光滑的质量被造船家称为 “fairness”，因为它能最大限度地减少船舶在水中的阻力，所以被誉为 “fairness”。到了16世纪，欧洲造船业者已经开始依赖较小的比例尺图纸来进行绘制设计和施工文件。手持式的机械制图spline被发明出来，用来绘制重叠的正交投影和横断面图，从而确定了船舶的关键基础几何形状。然而，在将图纸转化为全尺寸的零件时，造船厂家至今仍采用传统的lofting技术，使用spline进行loft。

图4：德国运动学家和地质学家Ludwig Burmester设计的一组曲尺，如1904年Otto Lueger的Lexikon der gesamten Technik(技术词典)中的说明。 资料来源：Wikipedia contributors, “French curve”。维基百科撰稿人，”法式曲线”，维基百科，自由百科全书。

在这个时期，造船家并不是唯一使用spline的设计师。伟大的意大利文艺复兴时期的建筑师 Andrea Palladio 在他著名的论文《建筑四书》中描述了他是如何用一把灵活的尺子来描画古典柱子[v]的优美膨胀的轮廓。德国的运动学家和地质学家路德维希-布尔梅斯特（Ludwig Burmester）在1900年左右出版了一套标准化的曲线模板（见图4）（Lueger, 1904年）[vi]。每个卷轴状的模板都是各种数学曲线的组合。要使用它，绘图人员需要沿着工具的边缘找到一个接近的贴合点，然后重新定位，继续绘制切线曲线。在现代计算技术出现之前，曲尺是建筑师绘制任何不规则光滑物体时的首选工具。

汽车制造业 - 发明了计算机算法spline

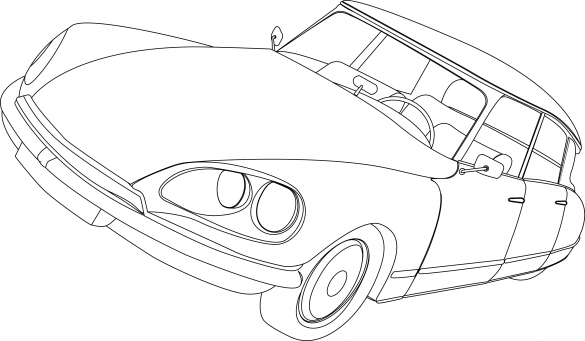
图5：1955年的巴黎车展上，雪铁龙的DS 19亮相。在车展的前15分钟内，就收到了743个订单。

现代计算机辅助设计（CAD）的诞生可以追溯到法国汽车制造商雪铁龙[vii]。到了20世纪50年代中期，该品牌已经巩固了其作为全球领先的创新者的地位。DS是雪铁龙的旗舰车型，它采用了前卫的技术，如自流平式水气悬挂系统，可将 “女神”（DS的发音与法语中女神的发音相同：déesse）抬起来，让她在法国战后颠簸的道路上毫不费力地漂浮在空中。

当它在1955年的巴黎车展上亮相的时候，这款身材魁梧的DS似乎已经做好了将法国带入太空时代的准备。哲学家罗兰-巴特(Roland Barthes)(1957年)将其形容为 “从天而降 “的超凡之物[viii]。事实上，在雪铁龙开始使用风洞设计的时候，车身的造型是由航空工程师安德烈-勒菲弗尔设计的。在意大利雕塑家Flaminio Bertoni的帮助下，DS也有了艺术气息。

DS不仅仅是流线型的产物。它也是第一辆量产的一体式汽车，这意味着圆形的金属表皮支撑着结构性负载，而不是依靠内部的钢架。在推出五十多年后，DS在其优雅的外形下解决了其独特的功能，至今仍是人们的偶像（尤其是设计师）。巴特斯将这种诗意的融合概括得非常简洁。

“(DS)激发人们的兴趣，与其说是由它的组件之间的连接，不如说是由它的内涵来激发人们的兴趣。众所周知，流畅性总是完美的属性，因为它的反面是技术性的人工组装操作。”

然而，像DS这样的突破性汽车的无缝组装，给雪铁龙带来了一个关键的挑战。它的解决方案将从根本上重塑设计和人类对几何形状和形式的控制。

除了全尺寸蓝图之外，雪铁龙和其他汽车制造商的设计过程主要依靠实物模型来进行概念开发，并在不同团队中保留、转换和共享汽车的几何形状。造型设计部门从制作新原型车的小尺寸概念模型开始。通过测量这些小型粘土模型上的偏移点，手工将曲面放大到全尺寸，然后重新绘制到真人大小的绘图板上。绘制的点用曲尺或弹性spline 尺进行内插，以得到一个最佳的近似值。胶合板的横截面将被切割出来，然后横向组装，形成一个相交的矩阵模板。骨架用粘土进行处理，并进一步雕刻，以创建一个详细的汽车主模型。在最终成型后，主模型将在熟练的泥塑师的手中继续进行精雕细琢，然后再将其定型，最后定型为生产所需。

设计师、工程师和机械师在设计零件和制造零件所需的工具时，可以参考主模型的几何形状（或其中一个副本）。要提取相关的几何图形，并确保其在整体装配中无缝配合，需要同样繁重的平移技术。要完成每个零件的设计，需要经过多次反复设计，这在很大程度上依赖于工人的技能、智慧和主观判断。然而，通常对几何图形的限定性解释带来了很大的不一致和人为错误的空间。公司需要一种通用的几何学语言来存储每个零件的数字，而不是依赖耗时和容易出错的手工复制过程。

到了20世纪50年代末，雪铁龙和它的竞争对手开始采用早期的模拟计算机—由于政府的支持—连接到机器上的模拟计算机，用于重复性地从钣金上压制车身零件的冲压模具。这些早期的数控机床需要将坐标以纸带打孔的形式输入，以引导刀具的路径，并在挖掘材料时引导其行程深度[ix]。线条、圆、抛物线和其他常规的几何函数可以从设计者的蓝图中准确地输入到机器中，但当时还没有可靠的自由曲线的方法，更不用说曲面了。

1959年，雪铁龙聘请Paul de Faget de Casteljau来解决这个缺失的环节。这位年轻的数学家刚从博士学习结束，他的任务是设计出一套方程系统，以便在设计人员和工程师之间可靠地存储和交流形状，并将其输入到驱动新的铣床的原始计算机中。起初，De Casteljau在这个问题上很纠结。他的顿悟是在他意识到，与其说曲线是由点来定义的，不如说曲线是可以通过操作曲线附近的几个点来精确地绘制和控制[x]。当这些影响点被移动时，曲线就会跟着移动，类似于移动固定船工spline的砝码的直观反应。

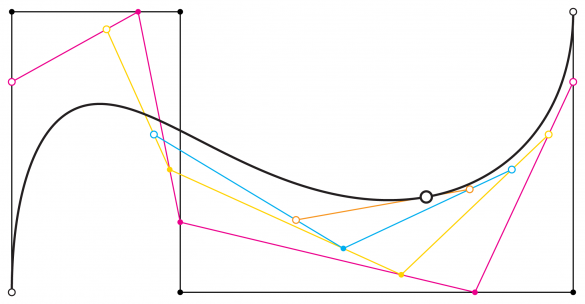
图6：在de Casteljau的方法中，沿每一个极点（黑色）按比例距离（即2/3的距离）创建点。新的极点(粉红色)连接这些点，然后再一次以相同的比例距离沿这些点创建点。新的极点和点被产生，直到最后剩下一个点为止。这个过程可以在每隔一段时间沿着极点的每一个细分点重复进行，以产生一条平滑的曲线。

De Casteljau的算法是一种递归插值的方法,已经存在于数学表达式Bernstein多项式中。描述这种微分几何的公式可能在数学上很高深，但可以直观地理解（见图6）。这些影响点被连接起来形成控制线，或者说是de Castelaju所称的 “courbes à pôles”。沿着这些极点按比例的距离（即2/3的距离）建立点。新的线将这些点连接起来，然后再一次以相同的比例距离创建新的点组。新的极点和点被产生，直到最后剩下一个点。从数学上讲，这个过程可以在所有的间隔上重复（由于计算的关系，可以无限次地重复），绘制出平滑的曲率过程。

1963年， de Casteljau 发现了这一发现后，立即赶到车间，仅凭数学数据就着手重建2CV的引擎盖，只是发现建模人员不愿意合作。De Casteljaus的理论在雪铁龙内部其他地方也遭到了质疑。仅仅十条线怎么可能实现他之前的其他人在六十页的方程中没有成功的尝试？模型师们对 de Casteljau 的极点嗤之以鼻，认为这似乎太过直观，声称任何人都可以发明它们。这怎么可能是一个值得称道的方法呢？如果有效的话，它有可能用冷硬的计算来取代汽车生产的手艺，从而使模型大师的影响作用被淘汰。这位年轻的数学家最终确实说服了公司，他的优雅算法是他们所寻求的终极解决方案，通过从数值数据中复制出越来越复杂的汽车零件，最终形成了GS的全身模型。无论是否欢迎，计算机曲线已经到来。

雪铁龙对de Casteljau的突破进行了严格的保密，他的研究结果在8年的时间里没有被公布。大约过了15年后，人们才把这一发现归功于他。然而，保密性并没有阻止他在雪铁龙的直接竞争对手雷诺公司的同行知道他的成就，尽管他的秘密算法本身并没有被发现。Pierre Bézier独立地重现了de Casteljau的成就，并在此过程中，使自己的名字成为曲线计算形式的代名词。

在20世纪60年代，雷诺面临着与雪铁龙相同的挑战。[xi] 最主要的是，如何将图纸板上的曲线转化为与早期数字计算机兼容的可靠准确的数学语言？雷诺还发现，在将每辆车的几何图形写入主模型，并将其传输到各个部件中的过程中，内部分歧、修饰、延迟和费用等问题都是充满了争议[xii]。 Bézier知道雪铁龙发现了什么，但他不知道是怎么做的。他解决这个问题的方法与de Casteljau的方法大相径庭，但最终的结果是相似的。早期，雷诺的人依靠经验观察和他的想象力。除了曲线绘图工具之外，他的部门已经开始使用简单的数学构造，就像笛卡尔的网格一样，在上面绘制出规则的数学曲线–弧线、椭圆和抛物线。这些曲线一旦被公式化地嵌入到二维网格中，这些曲线就可以通过数学上的变换来变形。但是，当处理更复杂的现实世界的三维曲线时–例如门板的边缘–就无法应用这种方法。根本的问题仍然是：如何定义三维空间内弯曲和扭曲的自由曲面？

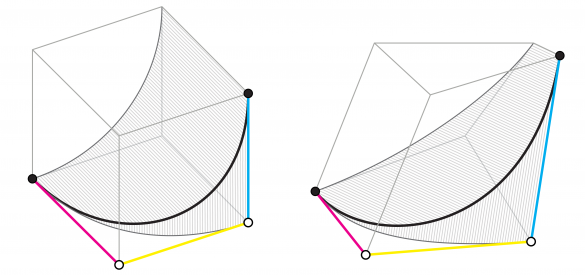
图7：Bézier的技术是由两个相交的圆柱面所产生的曲线（图中的阴影区域。为了清晰起见，省略了圆柱体外的部分）。 这些几何形状可以通过将它们包含在一个立方体中来进行数学定义（左图）。通过对立方体进行数学变换，里面的曲线也会被重塑（右）。在实践中，四个顶点之间的三个向量(粉色、蓝色、黄色)是唯一需要的参数。

Bézier设想了一个房间，在这个房间里，由弹簧、砝码和滑轮悬挂在地板、墙壁和天花板之间的柔性金属挤压物。尽管这个想象中的装置不切实际，但事实证明它在概念上是有用的。一个三维参数曲线可以表示为两个圆柱体的交点（见图7）。这些圆柱体的中心点和弧度点对应于立方体的顶点，包涵了其中的曲线。Bézier发现，通过对外立方体进行数学变换，他可以控制内部曲线的变形。随着他的想法的发展，他发现只需要立方体的三条相连的边就可以构造出不规则的曲线，而且他可以把它们组成多项式。如果要做更复杂的曲线，只需要更多的相互连接的线就可以了。

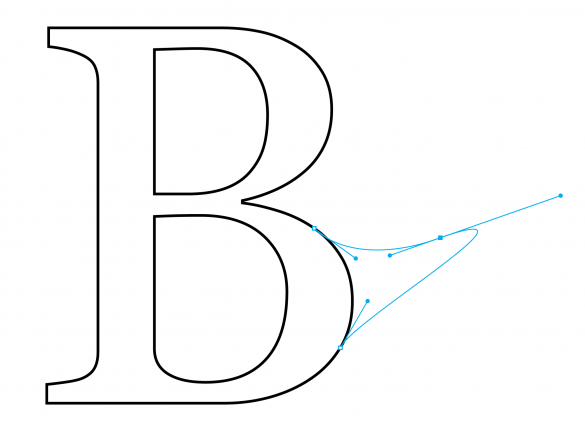
图8：Bézier cubic spline构成了PostScript和TrueType等桌面出版标准的主要部分。

到1966年，Bézier取得了与de Casteljau的courbes à pôles相同的结果，但与他的竞争对手不同的是，雷诺允许他发表他的发现。Bézier发明了以他的名字命名的计算机曲线。后来，这两个人的方法在数学上得到了调和，并被广泛被引用。后来，他们的几何学方法被纳入主流计算，直接使各个设计领域都受益匪浅。比如说，平面设计师们都会认识到贝齐尔曲线，在Adobe Illustrator这样的软件应用中，通过直观地点击和拖动顶点，就能顺利地绘制出图形。事实上，Adobe公司决定将其Postscript语言（以及苹果公司的True Type）建立在cubic Bézier曲线的基础上，导致了20世纪80年代的桌面印刷革命。它彻底改变了排版技术。普通电脑用户可能不知道，贝齐尔曲线如此优雅地描述了字体的弧形轮廓，使文字在任何比例下都能流畅地打印出来，同时消耗的存储空间几乎可以忽略不计（见图8）。

当然，汽车作为一种三维形式，并不仅仅是由一系列的复合曲线来定义。例如，钣金车身板，几乎每一点的曲率都是不同的。只定义每个零件的周长曲线并不能描述其内部轮廓。为了构造自由曲面，Bézier发现参考一种古老的铸造技术是有用的，它是用来在铸件上产生可变曲面的。将沙子装入一个敞开的木箱中。箱子的两个对立的顶部边缘是弯曲的，这样，当木板或模板拖过它们时，就会刮掉剩余的沙子，留下一个光滑的弧形表面。

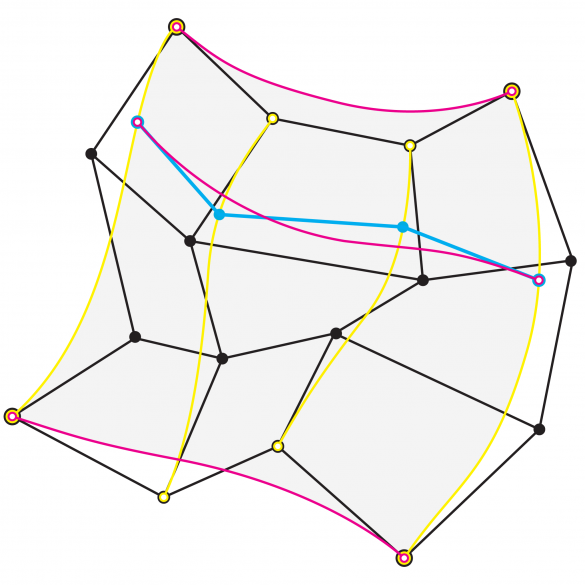
图9：Bézier将多项式曲线组合成三维曲面。以一个点的网格（黑色）为例，他在一个方向上建立了一组曲线（黄色）。沿着这些轨道等比例的点(蓝色)形成了向相反方向行驶的曲线(粉红色)。在每一个比例的距离上递归扫过这些轨道，就定义了一个曲面。底层的点的 “网 “可以很容易地、直观地处理，从而形成一个曲面。

Bézier推测，只要能在模板被拖过导轨时调节模板的形状，任何曲面都可以在一次稳定的扫描中形成。他再次制定了他的假设模具的数学结构（见图9）。Bézier利用他新发现的曲线来勾勒出箱体的两个弧形外缘。在这两条曲线之间，插入另一对曲线，在一个方向上产生四条独特的曲线。沿着这四条曲线中的每一条曲线的等比例的点可以连接起来，形成另一条横向的曲线（类似于模板在外轨之间拖动）。当横向曲线穿过四条导向曲线时，形状沿着它们变形，并定义了一个光滑的自由曲面的轮廓。控制点的矩阵形成了一个底层控制网，其顶点可以很容易地被移动来塑造和雕刻所产生的曲面。和de Casteljau一样，Bézier最初也遇到了来自高层管理人员对他的想法的抵制，他们告诉他：”如果你的系统有那么好，美国人就会先发明它！” 事实上，当时美国人还没有这样做，但通用汽车后来在计算机spline的发展过程中扮演了重要角色。

通用汽车公司当时的困境与法国汽车制造商的困境相似。到了1959年，该公司已经获得了数控铣床，但缺乏一种数学语言来输入流线型汽车的复杂形状，而这些汽车的尾翼和造型都是太空时代的尾翼的造型。Carl de Boor，通用汽车公司的研究人员，设计出了一种用于B-splines的递归方法，这是一种相当隐晦的数学函数，由I. Schoenberg在20世纪40年代首次提出（尽管数学发展可以追溯到19世纪），用于顺利地—尽管很费力地–绘制精算数据的图形。在GM公司，B-Splines的强大灵活性和卓越的控制力通过递归计算速度真正释放了出来。

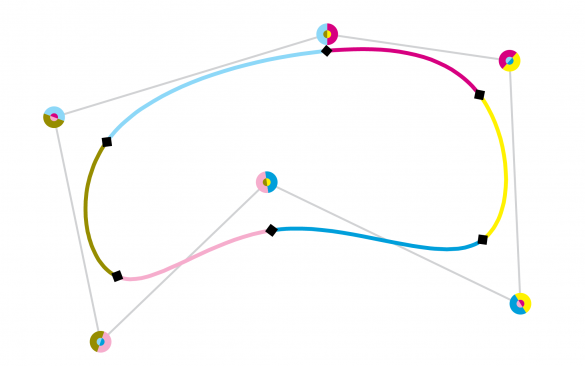
图10：闭合的 cubic B-splien。六个曲线段分别由四个点控制（每个控制点的颜色相对面积代表影响的大小）。事实上，每个节之间的曲线段（黑钻石）共享受其他曲线段影响的点，将它们融合成一条连续的平滑的spline。

与Bezier曲线一样，B-spline也是由一组相连的控制点控制的。B-spline中的B代表了它的多个基础函数。每一条曲线都定义了沿spline的重叠部分。重叠的子曲线被修剪，并以均匀的间隔捆绑在一起，贴切地称为 “knot”。每个基础 “段 “除了一个控制点外，其余的控制点都与相邻的控制点共享（见图10）。这个属性将它们平滑地融合在一起，成为一个spline。移动一个控制点只影响到最接近它的线段，因为根据基础函数的曲线公式，它的影响降为零。这样，当控制点被移动时，可以对一个区域进行局部控制，但不会改变spline的其他部分。因此，B-Spline，就像它的物理名称一样，更加精确和可控。也可以将B-spline闭合，形成一个循环。在数学上，后来发现B-spline是对Casteljau算法的概括，包括它和更大范围的几何图形。它也含了Bezier曲线。[xvi]

航空航天 - 寻找通用语言

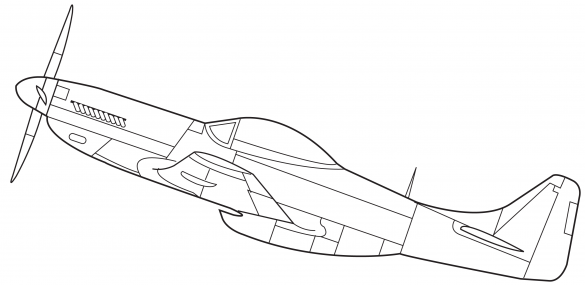
图 : Mustang P51的几何图形是以数字形式存储在表格中，而不是纸质蓝图。

在航空航天工业中，曲率是最重要的，因为空气动力学定律要求设计者绘制出平滑的曲线，并按照严格的公差制造。当然，早期的航空工程师们自然而然地改编了历史悠久的海军技术，用于制作飞机机翼和机身。在CAD广泛出现之前，制图师们使用灵活的spline曲尺来绘制曲线几何图形。但是，航空航天设计师们还采用了其他经典的几何结构，这些结构可以追溯到1600年代。其中之一就是圆锥体。通过旋转一个平面，它与圆锥的交点线产生一系列的圆、椭圆、抛物线和双曲面（见图11）。设计师可以通过将切线圆锥段串联起来画出机身的横截面。一个有经验的制图师只需使用一把尺子，就可以从四个点出发，通过简单而又费力地反复交错和细分直线的过程来构造出这样的圆锥曲线–这个过程与弦乐艺术并无二致。[xvii] 然而，要顺利地将他们所绘制的点连接起来，仍然需要曲尺的帮助，将它们尽可能地贴合成一条平滑的曲线。

在第二次世界大战期间，在机库中loft飞机（很多术语和技术都是从造船业中继承下来的）成为一种战略负担。一颗炸弹就能把战术上至关重要的飞机的主模板毁掉。[xviii] 此外，图纸可能被盗取或拍照，无法加密。Roy Liming是二战期间的一名航空航天工程师，他在北美航空公司（战后成为波音公司的一部分）工作，该公司生产战斗机，如野马战斗机。通过将参数化的圆锥体转换为算法，每架飞机的关键几何形状可以用数字存储在表格中，而不是纸质蓝图。这变得很有优势，因为数字可以安全地存储，并且很容易传输。此外，它们提供了效率、准确性、可重复性和安全性。

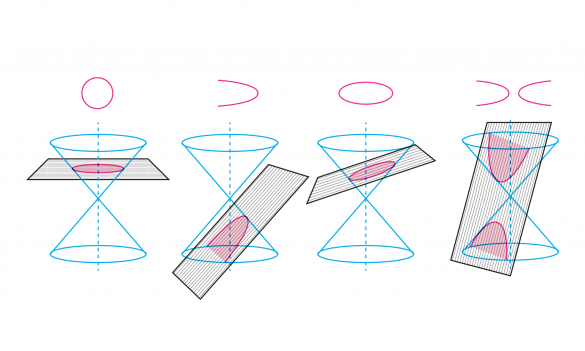
图11：圆锥是在平面和圆锥的各种可能的交点处计算出的数学曲线。

战后，像波音公司这样的私人航空航天承包商继续使用Liming的公式。到了1950年代中期，该公司已经开发出了自己的设计软件，在Liming的圆锥体基础上绘制机身。然而，十年后，在设计人员的办公桌前使用木制spline的情况仍然屡见不鲜。随着CAD的普及，各部门购买或开发了自己的专门软件来处理飞机的不同部件几何形状；例如，机翼设计需要连续spline来进行空气动力学分析。整个60-70年代，在设计、制造和装配飞机各部件时，这种方法的局限性越来越突出。

波音公司是早期计算机辅助设计中零散创新的一个缩影，由于各技术行业或部门的专业需求不同，计算机辅助设计往往会出现不同的变化。面对系统不兼容的问题，公司需要将其几何图形标准化，以便通过共享和协调设计几何图形和软件，实现团队的高效协作。1979年，公司任命了一个数学家小组，为11种曲线形式选择标准的表示方式–从线、圆到Bézier曲线和B-spline。

该小组很快就意识到他们的目标应该是一个单一的、全面的曲线表示，而不是十一个单独的曲线表示。他们设计出了合理的贝齐尔曲线–合理的意思是每个控制点的权重比可以变化（见图12）。可变权重比使得精确绘制圆锥体以及圆柱体和平面部分成为可能。几年前，S. Coons在锡拉丘兹大学的博士生们将B-Spline模型扩展到有理和非均匀模型。波音公司将非均匀的B-Spline—其结点沿曲线非均匀分布–纳入了他们的新表示方式。这种特性可以通过在一个位置放置多个结，在spline中引入尖角，有效地将曲线固定在该点上的角上。波音公司的团队找到了一种将有理Bézier曲线和非均匀B型曲线结合在一起的方法。到1981年，他们设计出了一种新的几何模型，可以满足波音公司的所有需求，从简单的线和圆，到最复杂的自由曲面和曲面。这种新的数学模型被称为非均匀有理基线花键，简称NURBS。

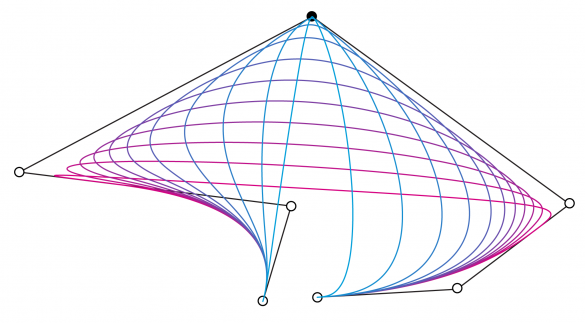
图12：NURBS的理性控制点可以单独加权。黑色点的权重从0.001（粉红色）到1,000（蓝色）不等。

NURBS很快被工程师和设计人员所采用。同年，波音公司的研究人员说服了由工业和政府机构组成的联合体–Initial Graphics Exchange Standard (IGES)，采用了NURBS。IGES成为美国标准协会（ANSI）CAD标准，使其成为CAD软件之间的数字交换语言。今天，各组织可以使用NURBS在同一软件中绘制机身、机翼和几乎任何设计部件，大大推进了设计团队、软件平台或公司之间的集成和协作。如果没有NURBS作为一种共享的几何语言，我们就无法想象现代制造业–无论是汽车、航空航天还是其他产品–由专业分包商和供应商组成的团队在共享的3D软件模型上进行合作，并进行高精度的合作。

动画 - 从拓扑学中解放出来

随着计算机辅助设计的成熟，计算机动画领域还处于起步阶段。尤其是皮克斯公司（Pixar）是CGI（计算机图形成像）的先驱，在1995年推出了第一部长篇电影《玩具总动员》。皮克斯的动画师们用NURBS几何图形为影片的角色和道具进行了精心的建模。然而，事实证明，用NURBS的曲面建模和动画化角色是非常困难的。NURBS仅限于拓扑学上的矩形表面，如扭曲的平面、圆柱体、球体和圆环形等（体积实际上是由修剪和弯曲的矩形表面产生的，其中一个或多个边缘连接起来形成一个封闭的形状）。但是，有机体很少有这么简单的形式。它们的拓扑结构是任意的，有许多孔、折痕和突起。要用NURBS来重现这些类型的物体，需要一种零散的方法。

《玩具总动员》中的每一个角色–比如牛仔娃娃Woody–都是由单独的NURBS表面拼接而成。每一个角色都必须经过巧妙的修剪和塑造，以创造出与下一个角色完美融合的假象。这个过程既昂贵、耗时，又容易出错。更糟糕的是，在动画制作过程中，人物的接缝处会出现笨拙地凸起或裂开的情况，需要花费数小时的人工逐帧校正。在下一部动画短片《Geri’s Game》（1997年）中，皮克斯尝试了不同的方法，用细分曲面来塑造人物的形象。[xxi]

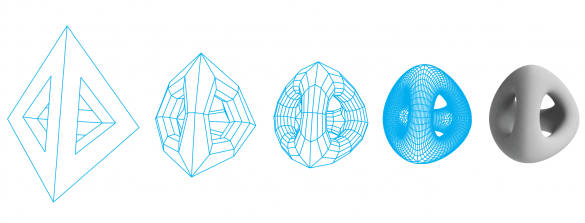
图13：细分曲面。原始网格被逐步细分为平滑形式，即使是复杂的拓扑结构也是如此。

Subdivision曲面建立在16年前Edwin Catmull（迪士尼和皮克斯动画工作室现任总裁）和Jim Clark（Silicon Graphics的创始人）的研究基础上，研究了递归统一的B-Spline曲面的可能性。细分曲面使建模师能够从单一的3D形式中雕刻出他们的角色，这就像雕刻师从一块泥土开始。在细分曲面的下方是一个控制多边形，类似于光滑物体的粗切面。计算机通过在多边形的顶点之间近似新的顶点，反复地对多边形的顶点进行细分。多边形被反复地细分，直到刻面细到消失成光滑的曲面（见图13）。随着现代计算机处理能力的提高，递归细分似乎是瞬时的。用户可以简单地移动底层控制网格的顶点，同时查看平滑化后的结果变化。

通过使用细分曲面，皮克斯的动画师可以更容易地塑造出皮肤和衣服不符合简单的正方形拓扑结构的角色。角色可以可靠地被动画化为奔跑、跳跃和蹲下，而不至于在接缝处散开。附加的算法允许通过将控制多边形的某些边缘标记为 “硬”，从而使表面产生褶皱。指甲或眼皮的边缘可以在不破坏与周围皮肤的连续性的情况下进行铰接和细节处理。皮克斯现在在其所有的动画电影中都依赖细分曲面，该技术已经成为建模和动画软件中的标准功能。

动画师向细分建模的迁移，是他们的行业技术与设计的分水岭。设计师和工程师继续青睐于NURBS，因为它提供了他们在精确制造现实生活中的产品所需要的精确曲率控制。动画师–他们只需要关注一个移动的形状如何在屏幕上出现–已经很高兴地放弃了这种控制，转而青睐于细分曲面提供的艺术灵活性和速度。针对航空航天、汽车和产品设计市场的软件提供了一系列基于NURBS的复杂的参数化建模工具，这些工具的外观和行为有点像细分曲面，但从根本上来说，它们仍然受制于NURBS的底层拓扑结构。

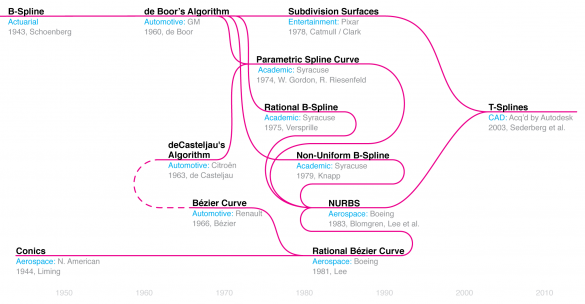
图14：T-Spline。虚线代表了通过数学归纳得出的后来的关系。

计算机spline的历史—-从严格的数学意义上说—-是连续的数学概括的记录(见图14)。换句话说，每一个继任的几何表示都包含和扩展了一个或多个前面的几何表示，其目的是为了更大的包容性。例如，NURBS可以表示早期的圆锥体、贝塞尔曲线和B-splines，以及简单的圆、弧和线。下一个合乎逻辑的步骤是NURBS和细分曲面之间的桥梁，因为它们有一个共同的共同祖先B-Spplines。这种重要的调和似乎是最近以T-Spline的形式出现的。[xxiii] 尽管从纯数学角度来说，[xxiv]T型线还不是NURBS的完美概括，但T-Spline似乎正处于广泛的商业化实施的边缘，在一系列行业中都有广泛的应用。它们与NURBS的前向和后向兼容，这意味着T-Spplines可以集成到现有的CAD/CAM工作流程中。开发商T-SPlines Inc. T-Splines承诺[xxv]，通过将NURBS的精度和控制与细分曲面建模的直观雕塑界面和拓扑自由度相结合，为设计者提供了一个卓越的3D工具集。

后续的发展最终将使设计师–或者说任何人–都能直观地塑造物体，而不必受制于技术上的繁琐和不灵活的混合不同表面的过程，由固定的结构几何图形构建而成。一旦出现这种情况，期望看到自由形状设计的整合、衔接和精细化程度会更高。2013年，3D打印成为了主流。这一趋势，再加上不断提高的计算能力，以及软件选择的激增–尤其是免费和开源的替代品–将使复杂的几何图形大众化，将使3D软件的用户群扩展到专业行业及其训练有素的软件操作人员之外。这种趋势是否会导致触觉计算机建模界面，就像折叠纸板、成型粘土或弯曲木条一样触手可及？spline的最新通用化使人类离完全掌握形式又近了一步。

关于雪铁龙DS，罗兰-巴特谈到了 “一种新的组装现象学，仿佛一个人从一个元素被焊接的世界进入了一个世界，在这个世界里，元素被并列在一起，并以其奇妙的形状并存，当然，这当然是为了让人准备好迎接更多的自然界的想法。” 巴特所设想的几何学奇异性正在迅速逼近。

建筑—后裔形式

事实证明，动画软件提供的逼真的光照、材料和渲染质量比标准的CAD软件包所能达到的可视化效果要好。因此，自20世纪90年代以来，建筑师们就开始使用动画软件作为设计工具。[xxvi]一个早期的震中是南加州（并非巧合），在那里，好莱坞特效软件的主要倡导者Greg Lynn创造了blob架构这个词。[xxvii] 除了逼真的渲染能力，动画师的工具集–特别是细分曲面–为冒险的设计师们提供了雕塑的自由度，让他们可以不受欧几里得拓扑结构的限制，轻松地开发出不受约束的设计。因此，从那时起，闪亮的无定形形式从建筑学校中涌现出来，伴随着大量的概念论述来证实这些新的形式方法。

尽管在计算机中制作异域的数字形式越来越容易，但对于实践中的建筑师和工程师来说，一个挑战依然存在：主要是，如何可行地构建这样复杂的几何体？在这方面，建筑、工程和建筑（AEC）已经取得了巨大的进步，但技术水平却落后于制造领域，因为在制造领域，曲率是必须的。但是，这也是可以理解的。建筑物通常是一次性设计的，而不是在密封控制的工厂里，由机械手在海外大量生产。AEC行业并不像汽车制造业那样整合，只有少数几家公司控制着庞大的市场，花费数十亿美元的研发预算来开发单一的产品。促使像Casteljau和Bézier这样的早期先驱者提出的挑战–利用计算将不规则的形式合理化成离散的部件，由早期的计算机化机床制造–目前仍在建筑领域展开。对于以细分面进行流畅设计的建筑师来说，一个关键的挑战在于将概念形式的无限拓扑结构合理化为可以制造和组装的离散构件。BIM（Building Information Management）和其他基于参数化的NURBS建模软件通过逻辑关系组织三维建筑几何形状，通过在一个共同的三维平台上整合制造和设计，有望使二维文档变得过时。由于与NURBS不兼容，BIM工具到目前为止还缺乏细分面建模，但也许不会太久。

弧形建筑（Hadid、Gehry等）还远未成为主流。它需要专业的软件知识来设计（更不用说合理化和建造）这种表现主义的作品。尽管是用电脑设计的，但由爱好曲线的名人建筑师设计的建筑，需要额外的设计人力和3D CAD技术，尤其是与传统的平面和正交的建筑相比。由于它们的建造难度大，通常来说，成本也更高（因此，复制和模仿的成本也更高），所以它们更独特，（可以说）更有价值。然而，进入这个精英领域的门槛—-对如何生成和处理复杂几何图形的技术知识—-正在不断降低，越来越强大和用户友好的三维建模界面也在不断降低。这些通过将复杂的数学spline操作抽象化，将其重新编码成一组工具，模仿我们在现实世界中的制作经验：loft, trim, extrude, lath, sweep, weld, sculpt等。T-Spline和其他潜在的泛化细分面和NURBS将消除一个重要的障碍，也许最终使自由形式的建筑物的设计和建造变得微不足道。

合理的比例和规律性是古典美学的基础，其前提是对美和自然秩序的经验性定义。这些定义在各种新古典主义的复兴中被编纂、重复和重新解释。spline也拥有可量化的参数，可以验证其美学上的愉悦性。order、tangency和fairness是技术术语，定量地描述了spline的数学连续性。这些变量控制了曲率变化的扭曲，人眼可以识别为凸起、凹痕或折痕。本能地，我们对这些特征的感知能力很强–比如说，在欣赏希腊雕像的扭曲的躯干时。汽车制造商仍然依靠人的眼睛来检查车身，在汽车下线之前，他们会将汽车通过隧道中的条形灯，确认车身的反光是否光滑。

spline和流动的表面不容易让人产生规则和范式，因为它们似乎缺乏有限的尺寸–边、角、边、顶、墙等。在讨论建筑设计时，我们也很难用文字来形容曲率。像造船、汽车和航空设计这样的性能驱动型行业，更能理解曲率的可量化（更不用说高度市场化）的好处。研究spline的历史发展轨迹，可以为当代建筑形式的发展提供一个更全面的视角，作为人类几何学进步的一个延续。spline的每一次新的迭代都调和了不同的模型，使其向通用几何学迈进了一步。随着计算继续侵蚀建筑的形式限制，曲率很快就会变得不起眼，就像我们日常消费的许多塑料制品一样：一次性剃须刀、电脑鼠标、洗洁精瓶、水壶、塑料玩具等等…除去几何学上的矫情，建筑师们可能会因为其微妙的复杂性、结构的优雅，以及（我敢说）纯粹的美感而拥护这种spline形式。

[This article was originally published in the International Journal of Interior Architecture + Spatial Design, Applied Geometries (Jonathon Anderson & Meg Jackson, 2014).]

i See vii and xiii.
ii Woodman, Peter C. (1985). Excavations at Mount Sandel, 1973-77, County Londonderry (p. 197). London: H.M. Stationery Office.
iii Rieth, Eric. (2003). First Archaeological Evidence of the Mediterranean Moulding Ship Design Method, The Example of the Culip VI Wreck. Spain, XIIth-XIVth c. (p. 11). In Horst Nowacki & Matteo Valleriani (eds). Shipbuilding Practice and Ship Design Methods From the Renaissance to the 18th Century. Berlin: Max Planck Institute for the History of Science.
iv Nowacki, Horst. (2006). Developments in Fluid Mechanics Theory and Ship Design before Trafalgar (p. 8). Berlin: Max Planck Institute for the History of Science.
v Mitchell, Bill. (2003). Roll over Euclid (p. 355). In Frank Gehry, Architect. Jean-Louis Cohen (ed). New York: Guggenheim Museum.
vi Lueger, Otto. (1904). Lexikon der gesamten Technik und ihrer Hilfswissenschaften. Stuttgart, Leipzig: Deutsche Verlags-Anstalt.
vii Farin, Gerald E. (2002). A History of Curves and Surfaces in CAGD. In Handbook of Computer Aided Geometric Design. G. Farin, J. Hoschek, M.-S. Kim (eds). Amsterdam: Elsevier.
viii Barthes, Roland. (1957). Mythologies. París: Seuil.
ix de Casteljau, Paul de Faget. (1963). Courbes et Surfaces à Pôles (p. 45, Technical Report). Paris: Citröen.
x de Casteljau, Paul de Faget. (1999). De Casteljau’s autobiography: My time at Citroën. Computer Aided Geometric Design, 16.7, 583–586.
xi Bézier, Pierre. (1998). A View of the CAD/CAM Development Period. IEEE Annals of the History of Computing 20.2, 37-40.
xii Farin, Gerald E. (2002). Curves and Surfaces for CAGD (p. 1). San Francisco, CA: Morgan Kaufmann.
xiii Rogers, David F. (2000). An Introduction to NURBS With Historical Perspective (p. 36). San Francisco, CA: Morgan Kaufmann.
xivYoung, David. (1997). Garrett Birkhoff and Applied Mathematics. Notices of the AMS 44.11,1446-1450.
xv Schoenberg, I. J. (1946). Contributions to the problem of approximation of equidistant data by analytic functions, Parts A and B. Applied Mathematics 4, 45-99.
xvi Farin, “A History of Curves and Surfaces in CAGD,” 10.
xvii Morrison, Derek & Neff, Gregory. (1997). Lofting and Conics in the Design of Aircraft (pp. 222–227). Proceedings of the ASEE Illinois/Indiana Section Conference.
xviii Forrest, Robin. (1987). Forward. An Introduction to Splines for Use in Computer Graphics and Geometric Modeling. Richard H. Bartels, John C. Beatty, & Brian A. Barsky (eds). Los Altos, CA: M. Kaufmann Publishers.
xix de Boor, Carl. (2014).A Draftman’s Spline. Carl de Boor’s Homepage. Retrieved from: http://pages.cs.wisc.edu/~deboor/draftspline.html
xx Blomgren, Robert M. (2001). NURBS at Boeing. Retrieved from: http://www.smlib.com/white%20papers/nurbsatboeing.htm
xxi DeRose, Tony D., Kass, Michael & Truong, Tien. (1998). Subdivision Surfaces in Character Animation. Computer Graphics: Proceedings : Annual Conference Series : SIGGRAPH 98 Conference Proceedings, July 19-24, 1998. New York: Association for Computing Machinery, 1998.
xxii Catmull, Ed & Clark, Jim. (1978). Recursively Generated B-spline Surfaces on Arbitrary Topological Meshes. Computer Aided Design, 10(6), 350–355.
xxiii Sederberg, T. W., Zheng J. , Bakenov A., & Nasri A. (2003). T-splines and T-NURCCs. ACM Transactions on Graphics 22, 477–484.
xxiv Cashman, Thomas J. (2011). NURBS-compatible Subdivision Surfaces (Distinguished Dissertation) (p. 18). Swindon, UK: British Informatics Society Ltd, 2011.
xxv Autodesk Inc. (2011). Autodesk Acquires T-Splines Modeling Technology Assets (Press Release). xxvi Lynn, Greg. (1995). Blobs. Journal of Philosophy and the Visual Arts 6, 39-44.
xxvii Safire, William (2002, December 1) The Way We Live Now: 12-01-02: On Language; Defenestration. The New York Times.

DeBoor曲线算法

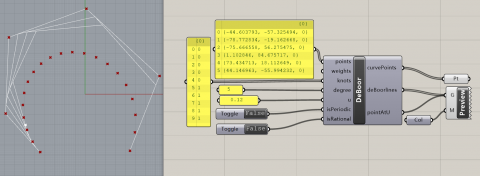
文中提到了DeBoor曲线算法, 它拓展了Bézier与de Casteljau 曲线.
本文的中文编辑马海东开发了Grasshopper插件.
下载地址: https://www.food4rhino.com/app/de-boors-algorithm

相关文章

• 建筑师为什么要会python编程?
• Caad4Rhino:建筑绘图工具插件
• Rhino及Bob McNeel的故事(转载)
• 曲线系列: 计算机曲线spline简史(转载)

建筑师编程课推广

ikuku精选课 Python4Rhino 建筑师编程课 2020.8.16开始线上直播！讲师:马海东

---