The engines don’t move the ship at all. The ship stays where it is and the engines move the universe around it. – Futurama

编辑: 马海东
编者按: 这篇《变换矩阵与投影》是编者对文章后面所列的参考文章,以编者的理解能力的汇总及解读.带着大家进入一个计算机图形学如何把3D物体展示在2D屏幕上的旅程.

在展开整个旅程之前,我先讲一个简单的案例来通俗的说明矩阵相乘意味着什么意思?

一个简单的矩阵相乘的例子

当地商店卖3种馅饼。当地商店卖三种馅饼。

• 苹果派每块3元
• 樱桃派每块4元
• 蓝莓派每块2元

而这是他们3天卖出的数量。

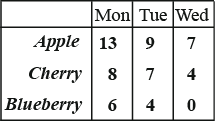
现在想想……周一的销售价值是这样计算的。

苹果派的价值+樱桃派的价值+蓝莓派的价值= $3×13 + $4×8 + $2×6 = $83

我们把价格和卖出的数量进行匹配，分别乘以每一个价格，然后将结果相加。

• 周一: 3×13+4×8+2×6=83元。
• 周二：3×9+4×7+2×4 =63元。
• 周三：3×7+4×4+2×0 =37元。

其中每一个价格与每一个数量的匹配很重要。

而这里是矩阵形式的完整结果。

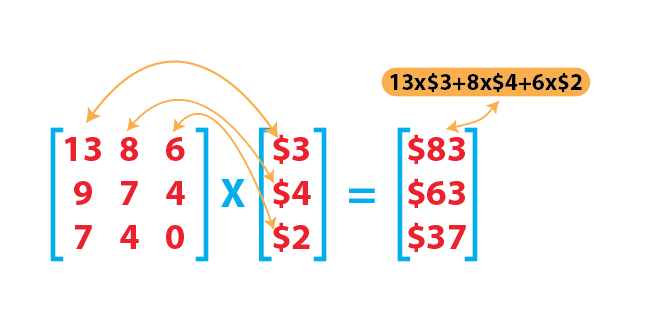
向量空间、齐次坐标与矩阵

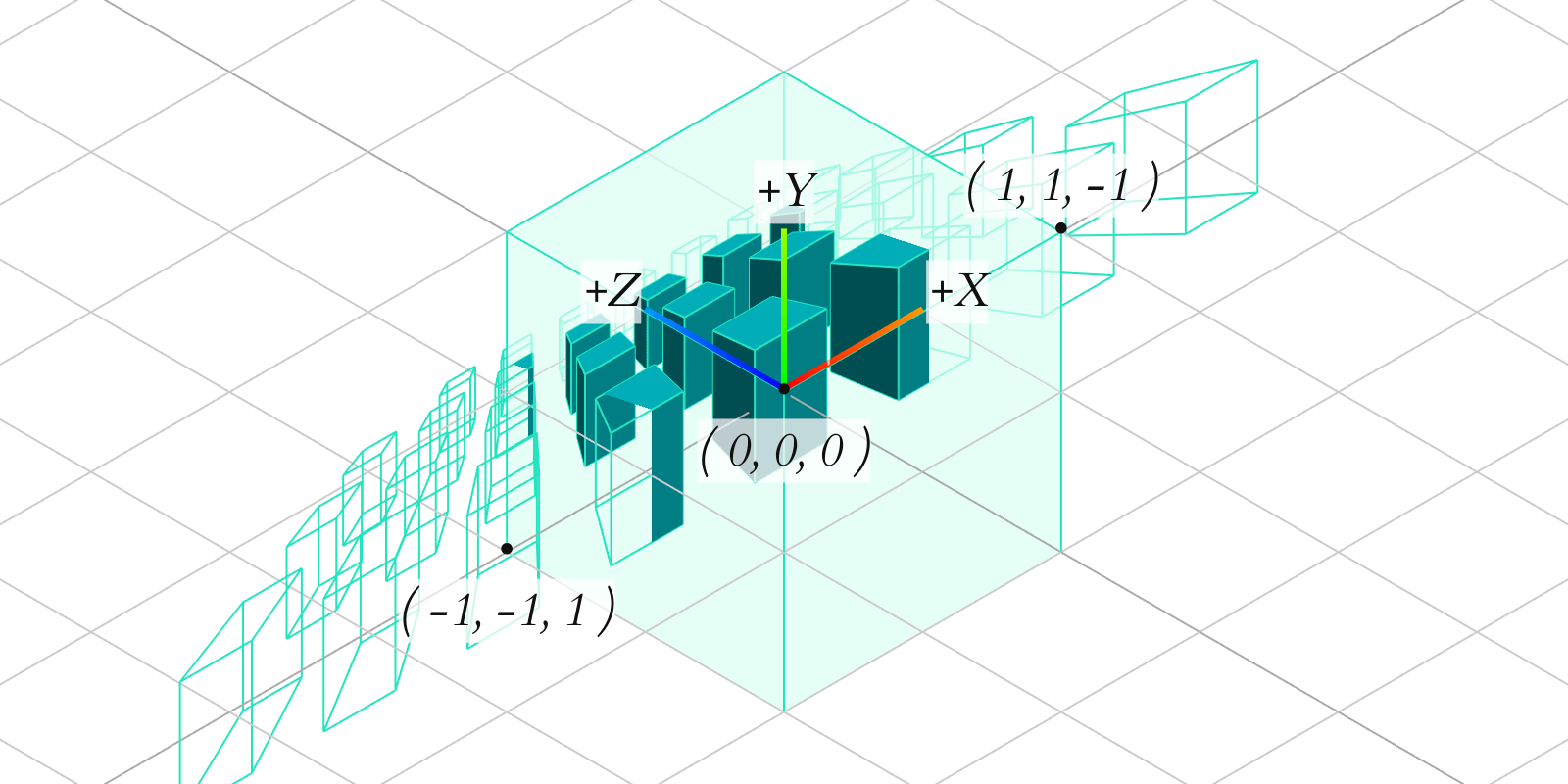
向量空间: 或者坐标体系, 一种数学结构，它是由给定数量的线性独立向量定义的，也称为基向量；线性独立向量的数量决定了向量空间的大小，因此一个3D空间有三个基向量(图1)，而一个2D空间有两个。这些基向量可以被缩放和相加来获得空间中的所有其他向量。

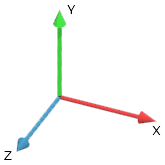
图1:标准右手三维坐标系统

todo: 图片, 空间中其他向量的表示

齐次坐标: 通常在计算机图形学中我们为了可以同时描述欧式空间及投影空间，我们还会引入齐次坐标(x,y,z,w), 来表示3维向量空间:

• 如果 w == 1, 那么向量 (x,y,z,1) 是3维空间中的一个位置.
• 如果 w == 0，那么向量(x,y,z,0)是3维空间中一个方向。

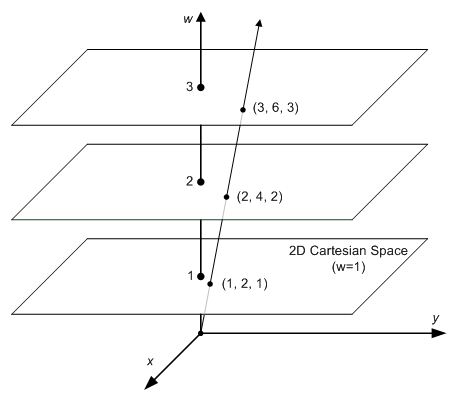
w等于或不等于0有什么不同吗？对于旋转来说，它没有任何改变。当你旋转一个点或一个方向时，你会得到同样的结果。然而，对于平移（当你把点向某个方向移动时），事情就不同了。平移一个方向是什么意思？ 没有任何意义。

4x4矩阵: 此外为了能在各种向量空间之间进行变换, 我们会使用(x,y,z,w)齐次坐标与4X4矩阵相乘进行变换。

[Matrix] x [Vertex] = [TransformedVertex]

通过以上这些数学元素,我们就可以把3D几何体展示在2D显示器上了.
它们依次经过从模型空间到世界空间的变换, 再从世界空间到视图空间的变换, 再从视图空间到投影空间的变换. 最终从投影空间变换显示到2D的显示器上.

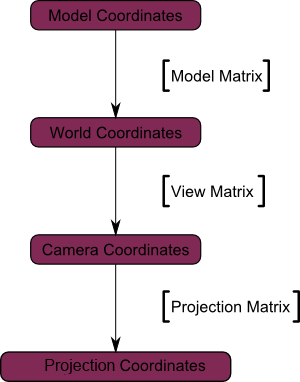
模型空间->世界空间

我们将3D模型存在的向量空间叫做模型空间(Model Space)，它用标准的右手三维坐标系来表示（图1）。

当一个设计师创作一个3D模型时，他创建的所有顶点和面都是相对于他所使用的三维坐标系(模型空间)。 如我们说一个点的坐标是(1,1,1),其中的数值是相对于其坐标系的原点而言的(图2).

场景中每一个模型在创建的时候都有自己的模型空间，如果你想让它们存在于任何空间关系中（比如你想把一个茶壶放在桌子上），你需要把它们转化为一个共同的空间体系（这就是通常指的世界空间）。

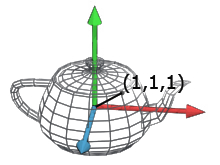
图2:茶壶的顶点在位置(1,1,1)。

现在，如果我们想把模型放到场景中，我们需要移动它和/或旋转它到所需的位置。移动、旋转或缩放一个模型，这就是我们所说的变换。当所有的对象都被转化为世界空间时，它们的顶点将相对于世界空间。

空间变换

我们可以把向量空间的变换简单地看成是从一个空间到另一个空间的转换。

我们可以把三维中的向量空间想象成三个正交轴（如图1）, 也就是我们用来作为其他一切物体(无论是几何体还是其他空间)的参考空间。

重点来了:
现在假设我们从一个”参照”空间开始，称它为空间A，其中包含一个茶壶。现在我们想应用一个变换，将空间A中的所有东西移动到一个新的位置；但如果我们移动空间A，我们就需要定义一个新的”参照”空间来表示变换后的空间A，让我们称这个新的参照空间为空间B（图3）。在变换之前，空间A中描述的任何点，都是相对于该空间的原点而言的（如左图3所述）。在我们应用了变换之后，现在所有的点都是相对于新的参照空间空间B（图3右）。

任何将空间A相对于空间B重新定义的操作都是一种变换。 请注意，在变换之后，空间A现在”消失”了，变成了空间B，或者更准确地说，它被重新映射到了空间B，所以我们没有办法对它进行任何其他的变换。

当我们应用变换时，我们将空间A向空间B移动，同时空间A中的任何东西也会随之移动。一旦我们移动了所有的顶点，这意味着所有的顶点表示为相对于空间B，我们就完成了变换。

如果我们需要再次在空间A中进行操作，可以对空间B进行逆向变换，这样做的话, 空间B将再次被重新映射到空间A中（此时，我们”舍弃”空间B）。如果我们知道这两个变换和它们的逆，我们总是可以将两个空间一一重新映射。

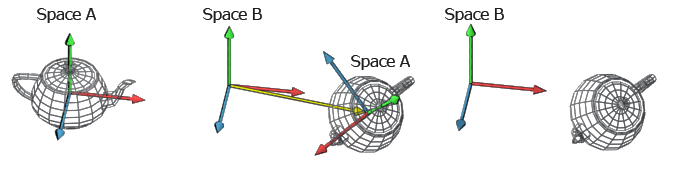
图3：空间变换

我们可以在向量空间中使用的变换通常有缩放、平移和旋转。
需要注意的是，每一次变换总是相对于原点的，这使得我们使用变换本身的顺序非常重要。如果我们先向左旋转90°，然后再平移，我们得到的东西与先平移再旋转90°的结果非常不同（图4）。

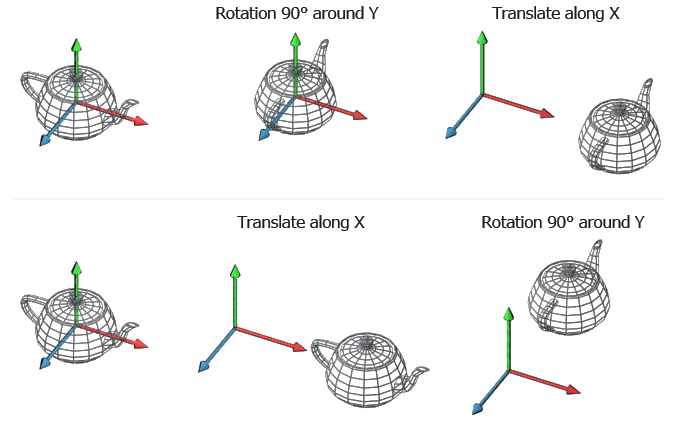
图4:同样的变换应用于不同顺序的不同结果。

变换矩阵

现在我们明白了变换是从一个空间到另一个空间的变化.

为了应用变换，我们必须将所有要变换的向量(齐次坐标)与变换矩阵相乘。如果向量在空间A中，而变换是描述空间A相对于空间B的新位置，那么在乘法后，所有的向量就会被描述在空间B中。

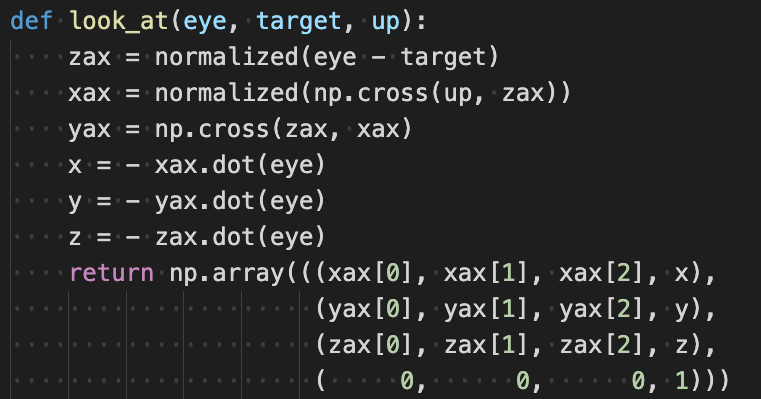
现在，让我们看看如何用矩阵形式来表示一个通用的变换。

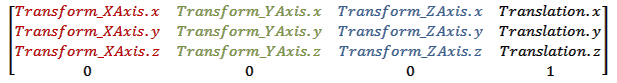
• 其中Transform_XAxis是新空间中的XAxis方向
• Transform_YAxis是新空间中的YAxis方向
• Transform_ZAxis是新空间中的ZAxis方向
• Translation是描述新空间相对于活动空间的位置。

有时我们想做简单的变换，比如平移或旋转；在这些情况下，我们可以使用以下矩阵，它们是我们刚才介绍的通用形式的特殊情况。

平移矩阵:

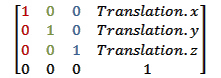
其中translation是一个3D向量，代表我们要移动空间的位置。
一个平移矩阵的xyz轴与之前的参照空间完全相同。

缩放矩阵:

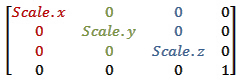
其中scale是一个3D向量，代表每个轴的比例。如果你读了第一列，你可以看到新的X轴它仍然朝向同一个方向，但它被scale.x缩放了。同样的情况也发生在所有其他轴上。另外，请注意平移列全部被设置为零，这意味着不需要平移。

围绕X轴的旋转矩阵:

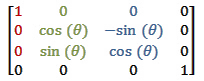
其中θ是我们想要用来旋转的角度。请注意第一列将永远不会改变，这是我们所期望的，因为我们是围绕X轴旋转的。另外，请注意将θ改为90°后，Y轴将重构为Z轴，Z轴将重构为-Y轴。

围绕Y轴的旋转矩阵:

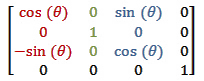
围绕Z轴的旋转矩阵

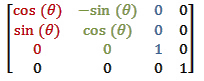
Z轴和Y轴的旋转矩阵与X轴矩阵的行为方式相同。

我刚才向你介绍的矩阵是最常用的矩阵。您可以通过将矩阵一个接一个地相乘，将几个变换连接在一起。其结果将是一个包含了所有变换的单一矩阵。

正如我们在变换部分所看到的，我们用来应用变换的顺序是非常重要的。在数学中，矩阵乘法不能互换的事实也反映了这一点。因此在一般情况下，Translate x Rotate与Rotate x Translate 是不同的。

变换矩阵相乘的次序是从右到左，所以如果我们想围绕Y轴向左旋转90°，然后沿着Z轴平移10个单位，其结果是:

[沿Z平移10]x[RotateY 90°]=[ComposedTransformation]。

一个变换矩阵的例子

让我们把一些数值放入矩阵其中，看看它是如何工作的。
假设我们想变换图5中的球体。为了简单起见，我们将只对球体的顶部顶点进行变换，它在模型空间中的位置是(0,1,0)。我们将计算它在世界空间中的位置。首先我们定义变换矩阵。假设我们要将球体放置在世界空间中，它将围绕 Y 轴顺时针旋转 90°，然后围绕 X 轴旋转 180°，然后平移（1.5，1，1.5）。

这意味着变换矩阵将是:

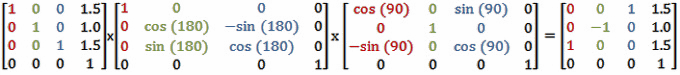
请注意，结果矩阵完全符合我们所介绍的通用变换公式。在世界空间中，X轴现在的方向是该空间的Z轴，因此现在是(0,0,1)。Y轴现在是倒置的，因此是(0,-1,0)。Z轴现在作为X轴的方向，(1,0,0)。最后，平移向量（1.5，1，1.5）。

一旦我们有了结果，我们可以乘以球体的任何顶点，将其从模型空间变为世界空间。让我们对顶点（0,1,0）进行变换。

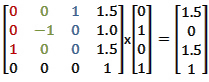
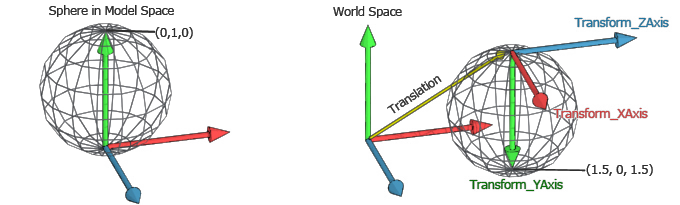
图5：从模型空间转换到世界空间的球体

世界空间->视图空间

当所有的物体都在正确位置的位置之后，我们现在要考虑如何将它们投影到屏幕上。这通常分两步完成。

• 第一步将所有对象变换到另一个空间，称为”视图空间”或者”相机空间”。
• 第二步是使用投影矩阵进行实际的投影。

为什么我们需要一个视图空间？视图空间是一个辅助空间，我们用它来简化数学运算，让一切都保持优雅，并简化为矩阵。

视图空间的定义: 默认状态下的摄影机设定为以相机原点为中心,负Z轴与相机的目标对齐。

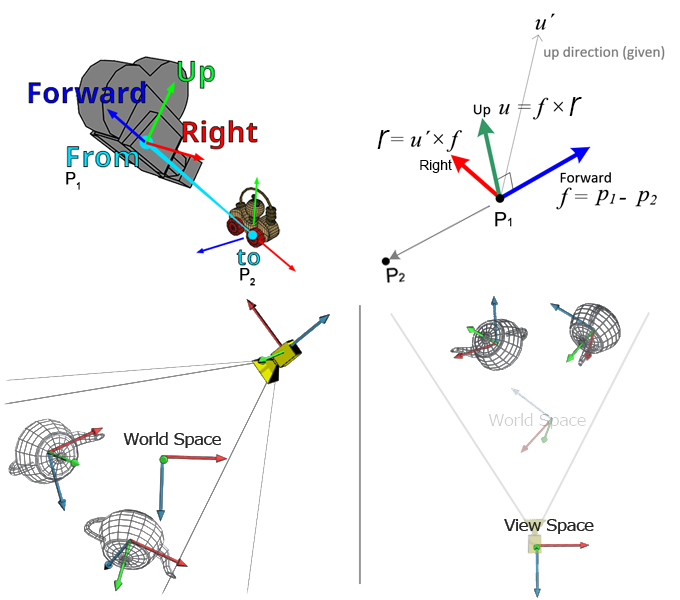
图8：左边是世界空间中的两个茶壶和一个摄像头；右边是所有的东西都被转化到视图空间中（世界空间的标识只是为了可视化空间转换)

视图空间->投影空间

现在场景已经在我们的视线范围之内,要做的就是把它投影到摄像机的2D屏幕上。在扁平化图像之前，我们还需要变换到投影空间。

投影空间: 这个空间是一个立方体，每个轴的尺寸都在-1和1之间。这个空间对于计算机图形学上对图像显示的剪裁来说非常方便（ 1,-1范围外的任何东西都在摄像机的视图区域之外, 可以不用被显示），并且简化了扁平化操作（我们只需要舍弃z值就可以得到2D图像）。

要从视图空间变换到投影空间，我们需要另一个矩阵，即视图到投影矩阵，这个矩阵的值取决于我们要执行的投影类型。最常用的两种投影是正交投影和透视投影。

要进行正交投影，我们必须定义摄像机能看到的区域大小。这通常用x轴和y轴的宽度和高度值，以及z轴的远近z值来定义（图9）。

图9：正交投影

给定了这些值之后，我们可以创建变换矩阵，将箱体区域重映射到立方体中。下面的矩阵是将View Space中的向量转换为Ortho Projected Space。

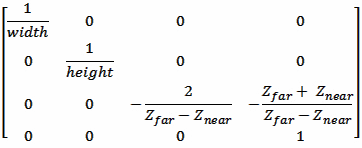
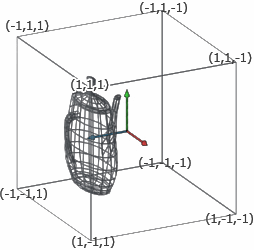
图10：从图9中的茶壶得到的投影空间。

另一种投影是透视投影。其思想与正交投影类似，但这次的视图区域是一个frustum.

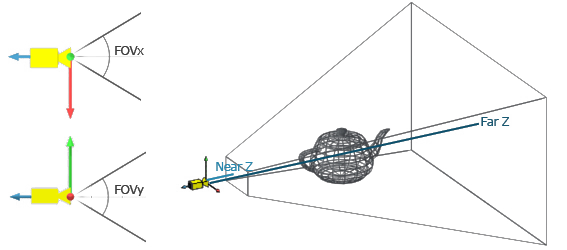
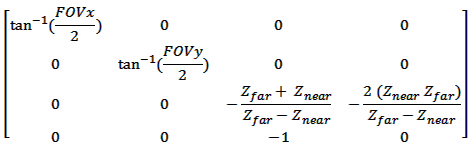
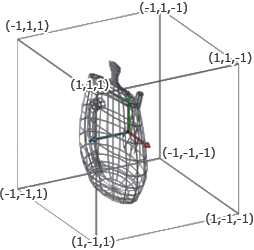
图11：透视投影

投影空间->屏幕空间

最后一步, 将所有从-1到1的范围重新映射到0到1的范围，然后将其缩放到视口宽度和高度，并将三角形栅格化到屏幕。

公式: [View To Projection]x[World To View]x[Model to World]=[ModelViewProjectionMatrix]。

reference

• http://www.opengl-tutorial.org
• http://www.codinglabs.net/article_world_view_projection_matrix.aspx
• http://ogldev.org/index.html
• https://www.scratchapixel.com/lessons/3d-basic-rendering/perspective-and-orthographic-projection-matrix/projection-matrix-introduction
• https://www.mathsisfun.com/algebra/matrix-multiplying.html
• https://jsantell.com/model-view-projection

相关文章

• 建筑师为什么要会python编程?
• Caad4Rhino:建筑绘图工具插件
• Rhino及Bob McNeel的故事(转载)
• 计算机曲线spline简史(转载)
• 漫谈算法设计(computational design)与脚本语言(grasshopper, python)
• 算法: 平面图自动生成(转载)
• 什么是齐次坐标?

建筑师编程课推广

ikuku精选课 Python4Rhino 建筑师编程课 2020.11.15开始线上直播！讲师:马海东

---