NURBS曲线DeBoor算法(Grasshopper数学插件)
16 June 2020
- 版本 0.0.2 alpha
- 版权 (c) 2019-2020 mahaidong
- Supported by ikuku.cn & caad.xyz
这个插件能做什么?
演示Nurbs曲线的DeBoor算法
仅仅靠自己的抽象想象力去理解不同的控制点位置(point)、权重向量(weight)和结点向量(knot)对NURBS曲线的影响是很难获得直观的理解与认识的.
这个grasshopper组件可以让你通过设定曲线的度数、控制点、重量向量和结点向量来演示如何生成NURBS曲线。其结果是让用户可以直观的看到最一般意义上的NURBS曲线的生成.
同时在曲线的绘制的时, 直接展示了与DeBoor算法相关的辅助线,及辅助线如何生成曲线.
DeBoor算法参考文献: https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/de-Boor.html
什么是DeBoor算法?
- DeBoor算法是DeCasteljau算法的B-spline版本
- 通过DeBoor算法可以精准的描绘B-spline
- 通过控制点及结点向量knot的值u,通过递归求得曲线上的点的位置
- DeBoor算法也可以用于Nurbs曲线的生成
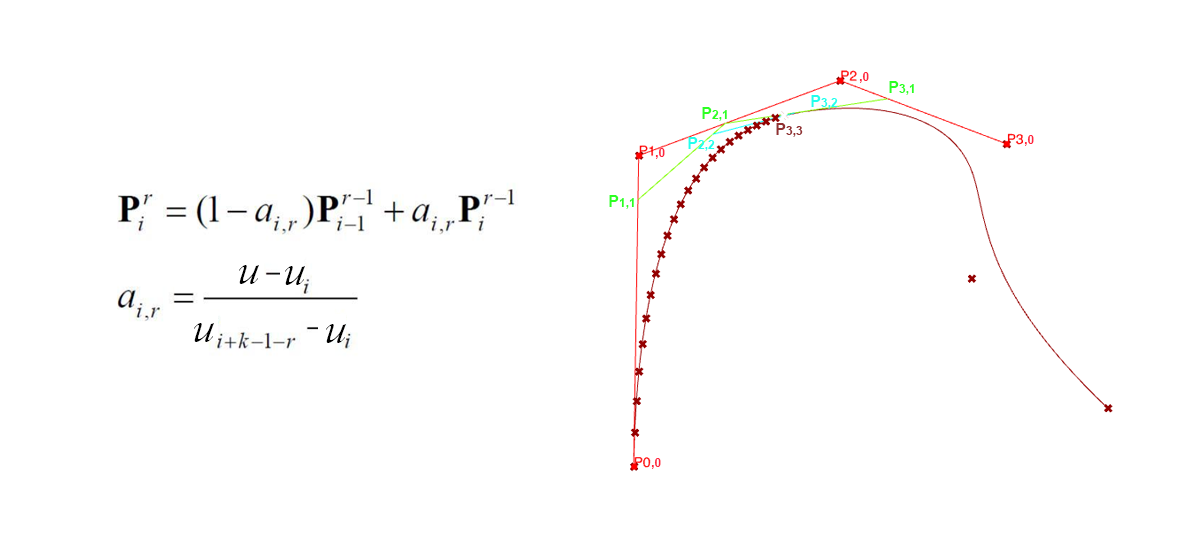
BSpline的DeBoor算法伪代码, python源码见github
Input: a value u
Output: the point on the curve, p(u)
If u lies in [uk,uk+1) and u != uk, let h = p (i.e., inserting u p times) and s = 0;
If u = uk and uk is a knot of multiplicity s, let h = p - s (i.e., inserting u p - s time);
Copy the affected control points pk-s, pk-s-1, pk-s-2, ..., pk-p+1 and pk-p to
a new array and rename them as pk-s,0, pk-s-1,0, pk-s-2,0, ..., pk-p+1,0;
for r := 1 to h do
for i := k-p+r to k-s do
begin
Let ai,r = (u - ui) / ( ui+p-r+1 - ui )
Let pi,r = (1 - ai,r) pi-1,r-1 + ai,r pi,r-1
end
pk-s,p-s is the point p(u).
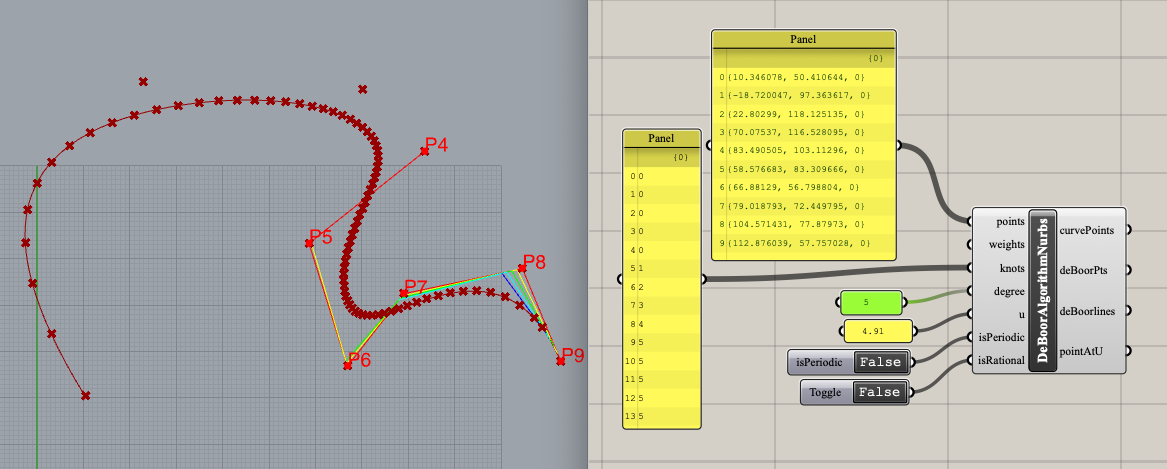
5阶BSpline的演示
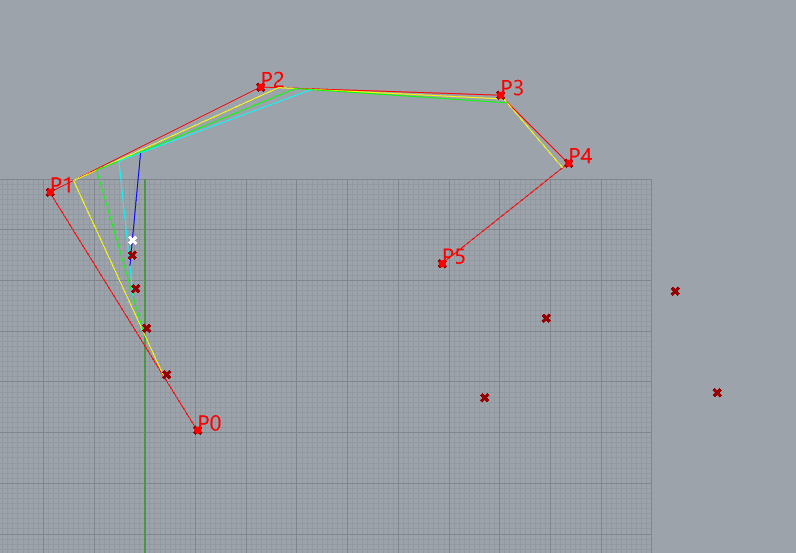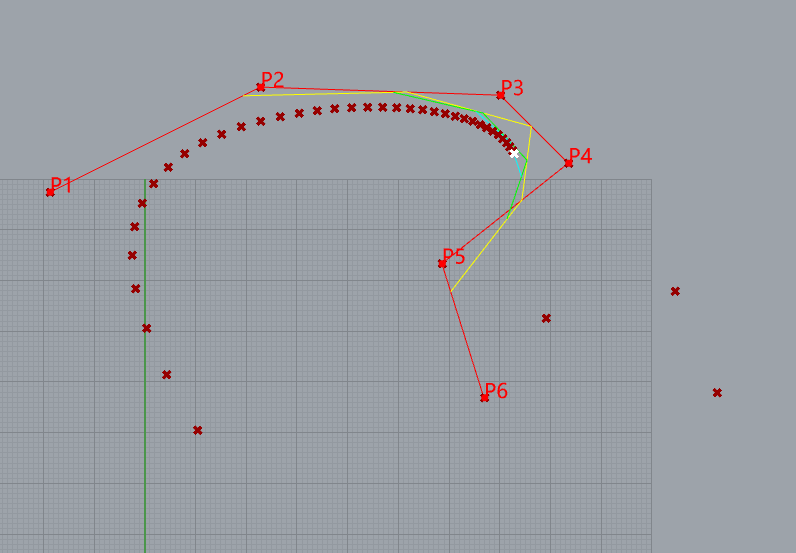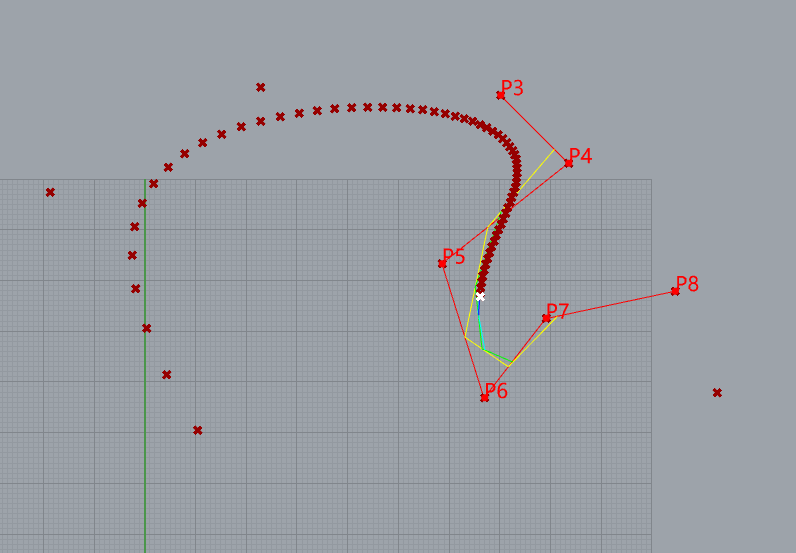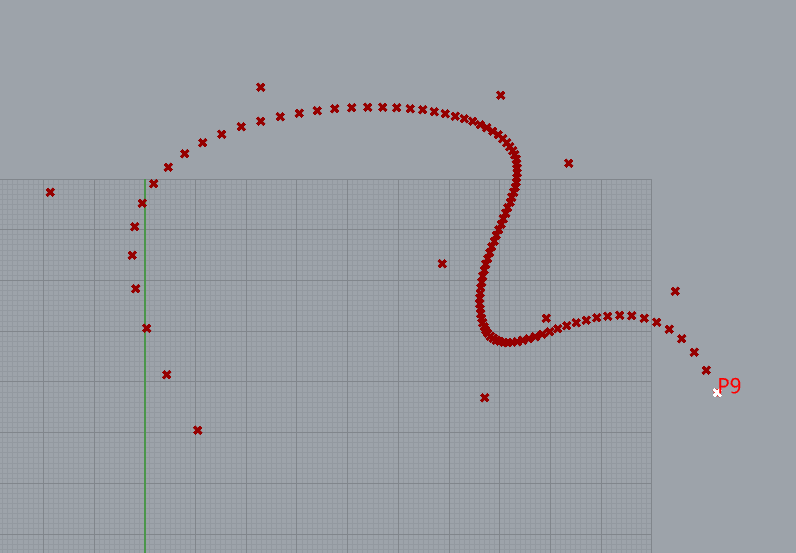
10个控制点
knots= [0, 0, 0, 0, 0, 1, 2, 3, 4, 5, 5, 5, 5, 5]
weight= [1, 1, 1, 1, 1, 1, 1, 1, 1,1]
NURBS曲线的DeBoor算法
De Boor的算法也适用于NURBS曲线。我们只需将每个控制点乘以它的权重,将NURBS曲线转换为4D B-spline曲线,在这条4D B-spline曲线上执行de Boor算法,然后将得到的曲线上的点的xyz除以w,就可以将曲线投影回来. python源码见github
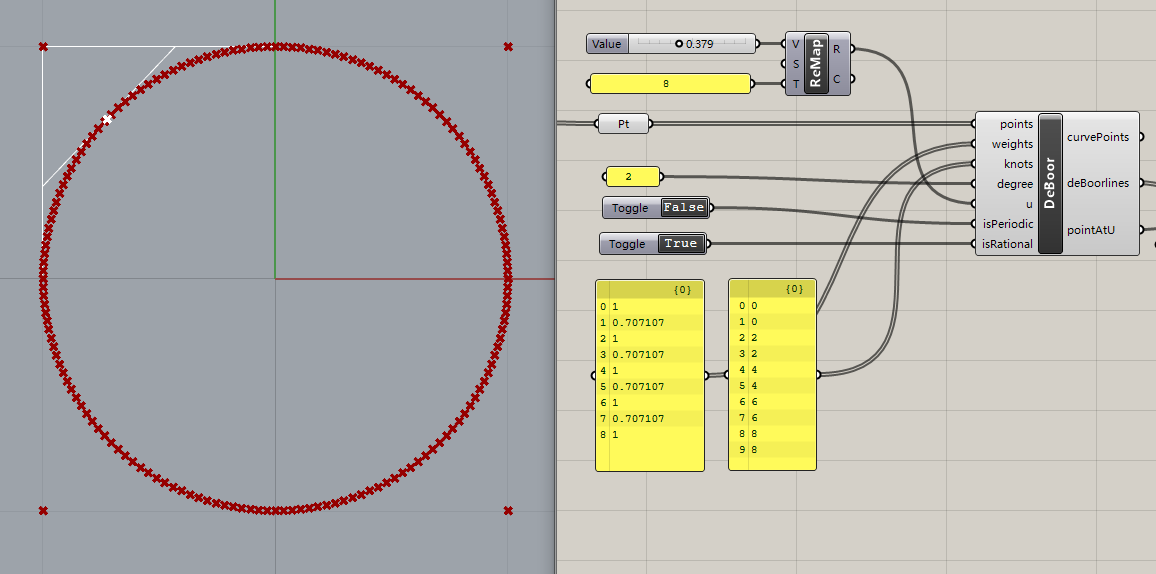
圆的Nurbs拟合演示
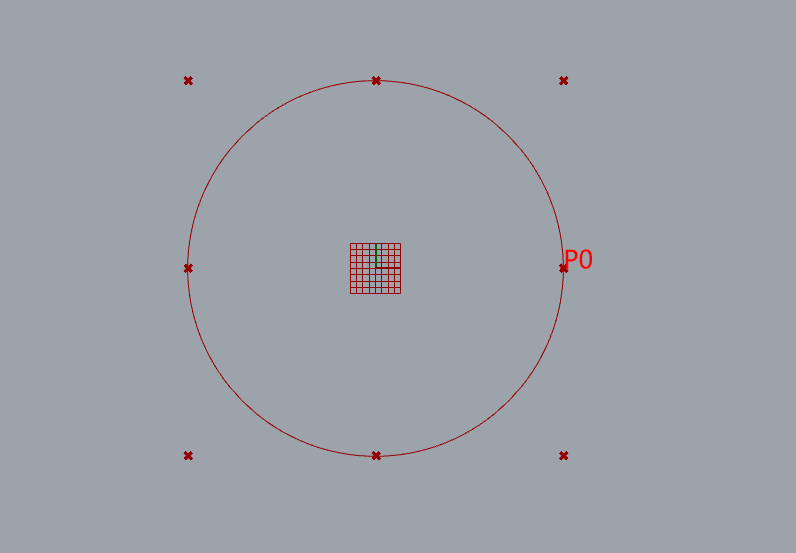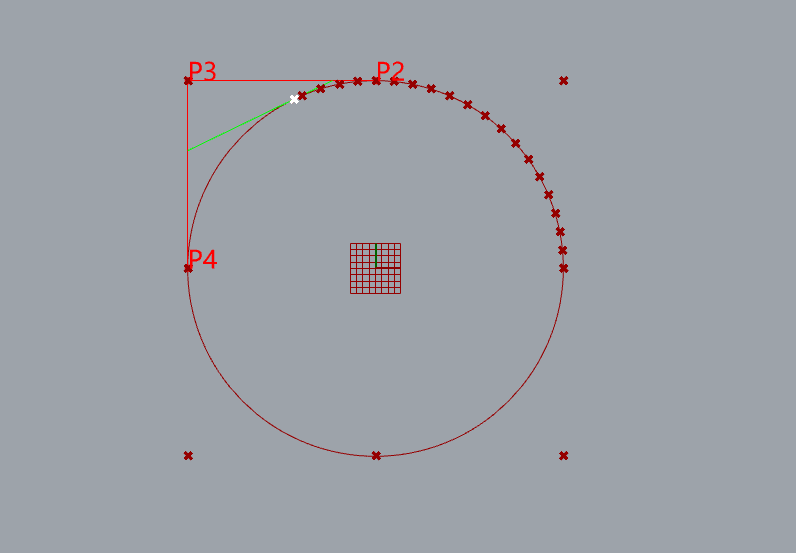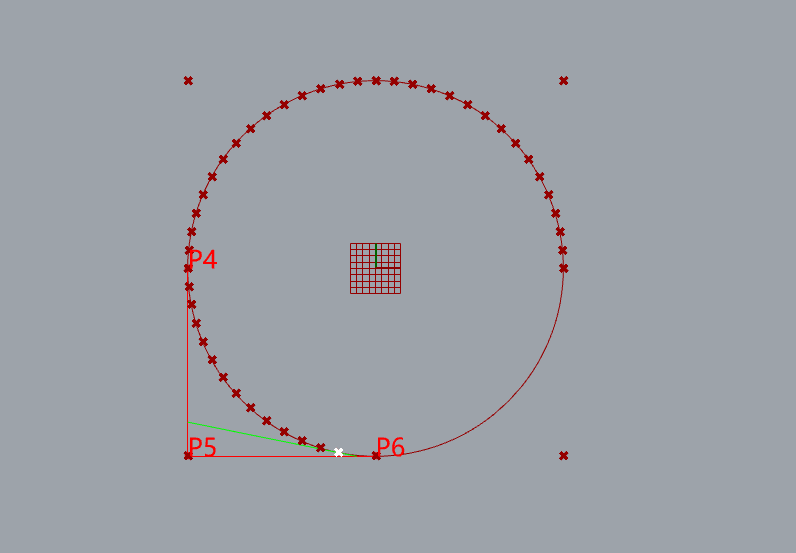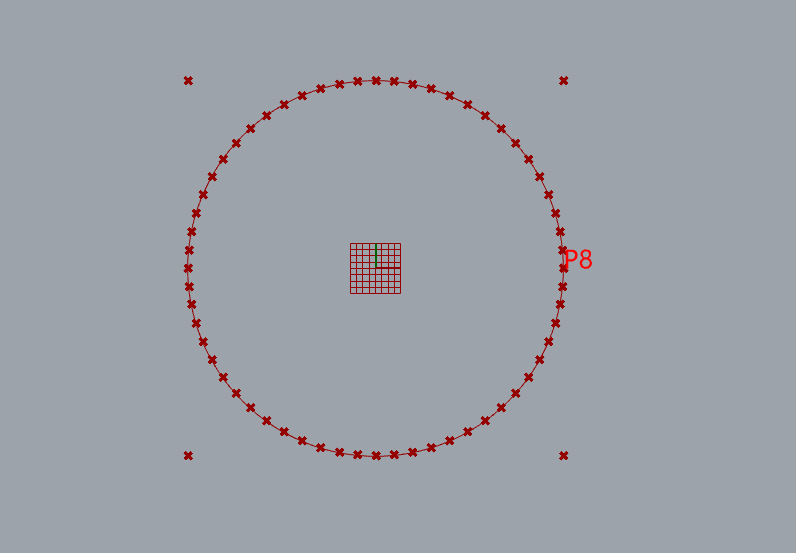
9个控制点
knots= [0, 0, 1, 1, 2, 2, 3, 3, 4, 4]
weight=[1, 0.707107, 1, 0.707107, 1, 0.707107, 1, 0.707107, 1]
演示Bezier曲线与Bernstein多项式
参数曲线的范畴
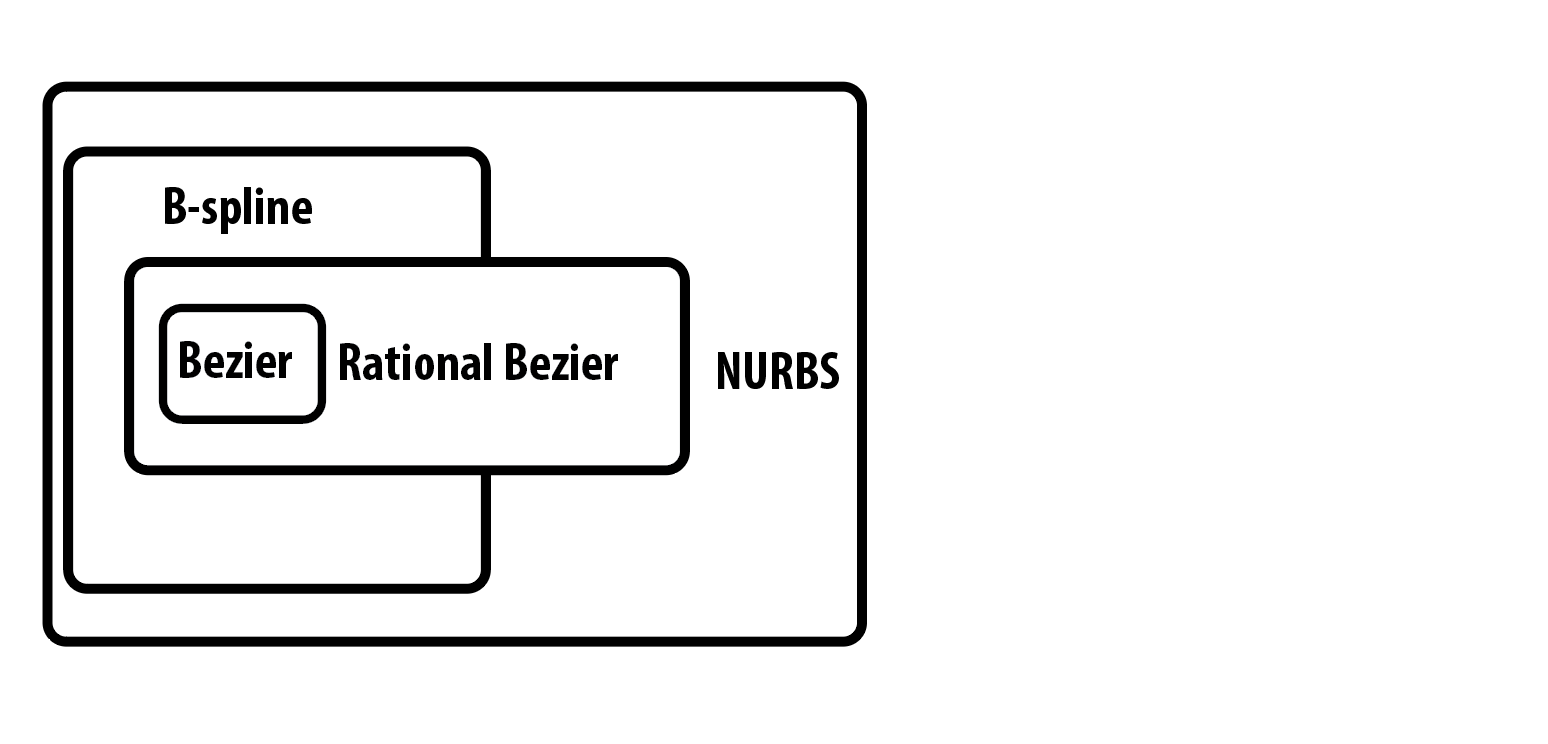
什么是Bezier曲线
Bezier曲线的数学基础–伯恩斯坦多项式–早在1912年就已为人所知,但直到大约50年后,法国工程师皮埃尔-贝兹尔(Pierre Bézier)才将这些多项式应用于图形,并将其广泛宣传,他用它们在雷诺公司设计汽车车身。这些曲线的研究最早是在1959年由数学家Paul de Casteljau利用de Casteljau的算法发展起来的,该算法是一种数值稳定的方法,用于评估法国另一家汽车制造商Citroën的Bézier曲线
关于Bernstein多项式的介绍见: http://www.ikuku.cn/post/1872817
Bezier曲线的数学公式
Bernstein多项式
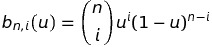
其中:
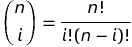
n阶贝塞尔曲线的定义
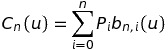
n=1:
当n=1的时候可以用来表示直线.
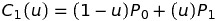
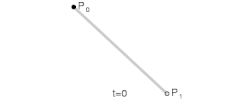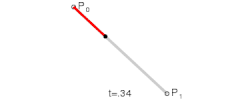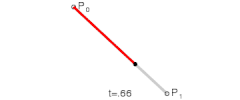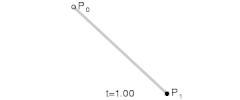
n=2:
当n=2的时候可以用来表示曲线.
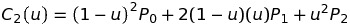
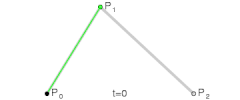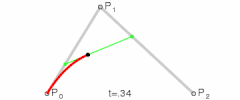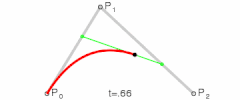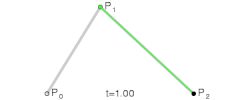
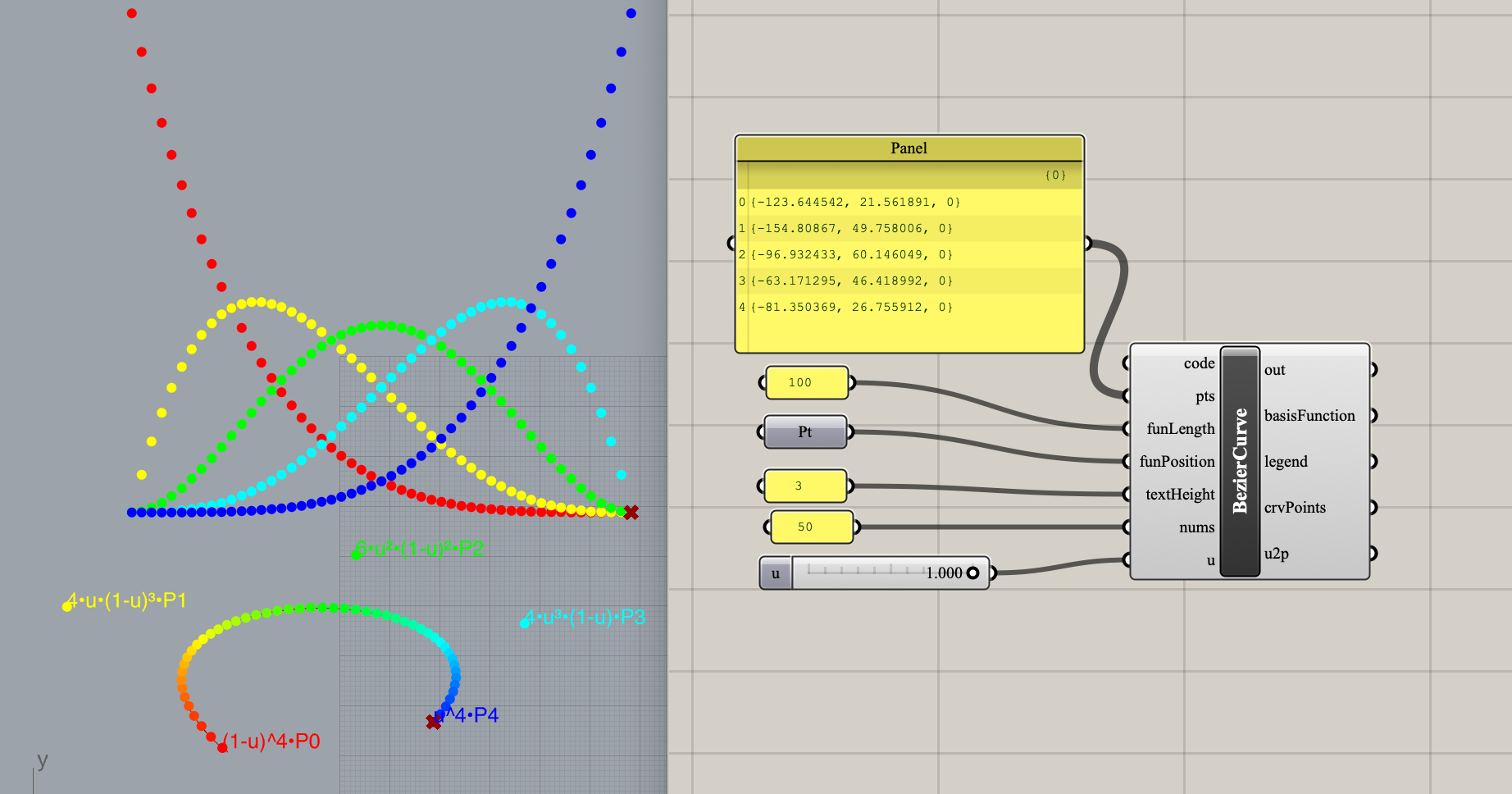
5阶贝塞尔曲线的演示
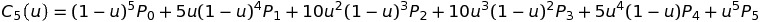
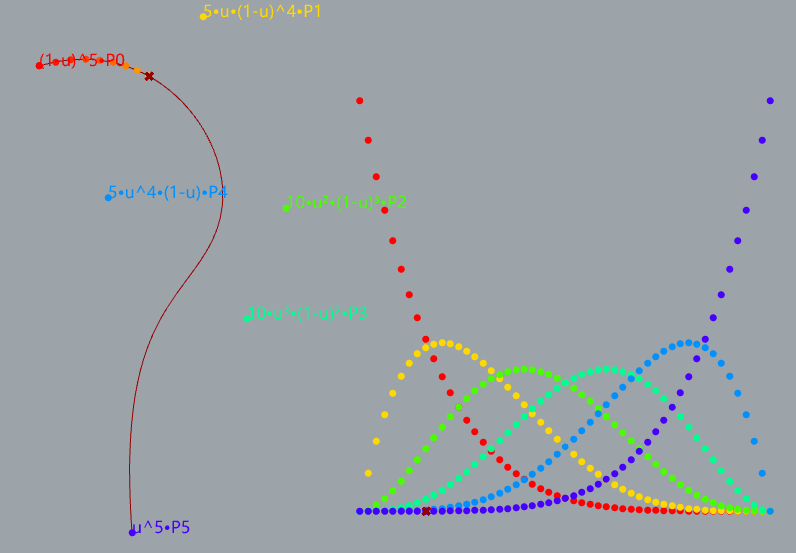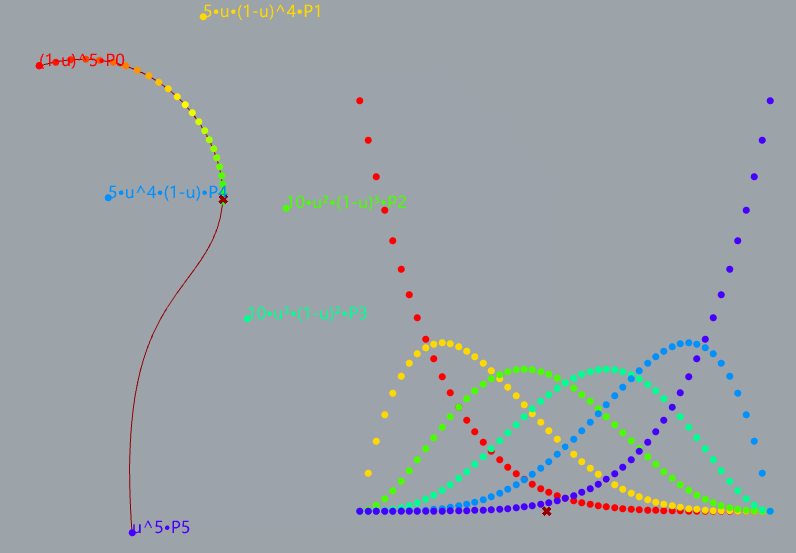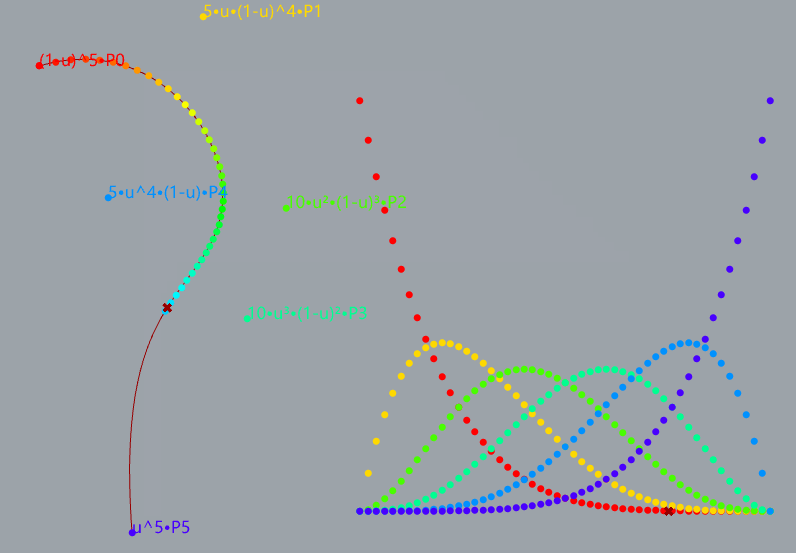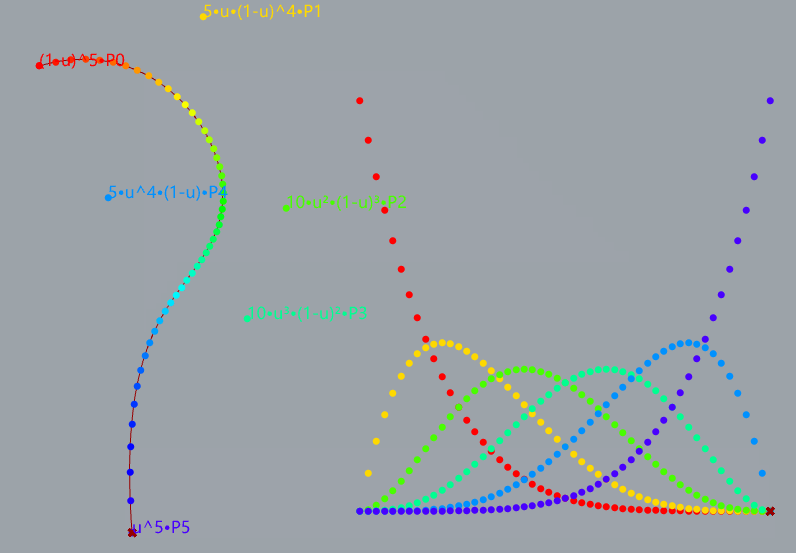
如何安装与使用?
Github源码下载: https://github.com/caadxyz/DeBoorAlgorithmNurbs
方法一
- 拷贝dist文件夹中的ghuser 文件到 User Objects 文件夹
- 打开dist文件夹中的案例文件 DeBoorAlgorithmNurbs.gh 查看演示效果
方法二
- 打src文件夹中的案例文件 DeBoorAlgorithmNurbs.gh 查看演示效果
b-spline:
nurbs circle:
bezier curve:
todo
- Single Insertion
- Inserting a Knot Multiple Times
- compute tangent and normal vectors at a point on a Bézier curve
- b-spline surface
- curve interpolation
许可证
你可以根据自由软件基金会发布的GNU Lesser General Public License版本3的条款重新发布它和/或修改它。
插件下载
food4rhino: https://www.food4rhino.com/app/de-boors-algorithm
Github源码下载: https://github.com/caadxyz/DeBoorAlgorithmNurbs
相关文章
- 建筑师为什么要会python编程?
- Caad4Rhino:建筑绘图工具插件
- Rhino及Bob McNeel的故事(转载)
- 曲线系列: 计算机曲线spline简史(转载)
- 曲线系列: 什么是Bernstein多项式?
建筑师编程课推广
ikuku精选课 Python4Rhino 建筑师编程课 2020.6.27开始线上直播!讲师:马海东

Comments
No comments found for this article.
Join the discussion for this article on this ticket. Comments appear on this page instantly.